如何估计模型中的参数

模型估计参数的前提条件：

• 估算的前提条件：自变量+给药方案+因变量+模型结构

• 对于药动学模型，自变量为采样的时间，因变量为样品的血药浓度，给药方案就是给药的时刻+剂量，模型结构就是我们期望使用的模型的实现（内置模型库，代码实现等）

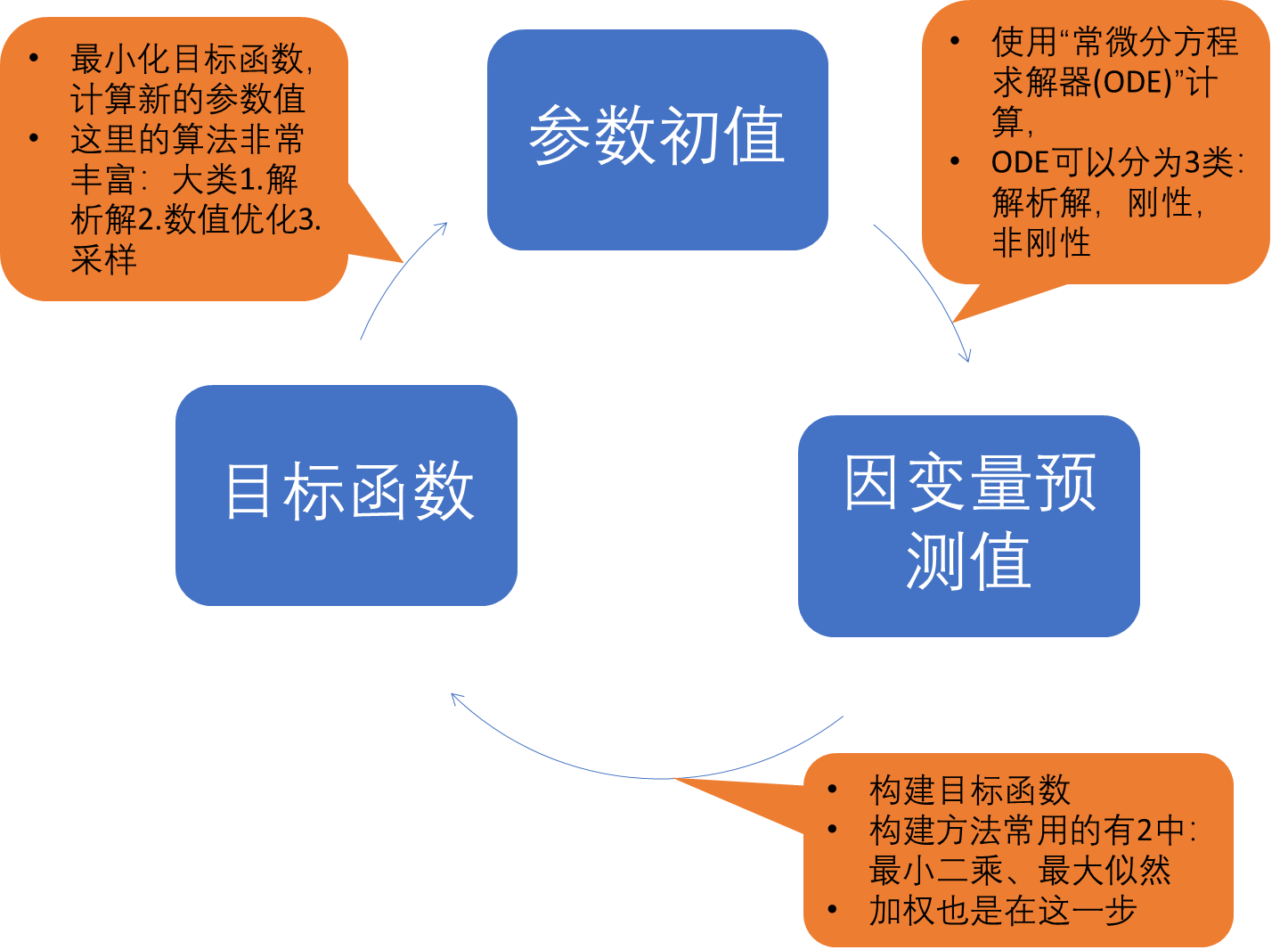
估计参数的工作的过程是：

1.  猜测一组参数值

	-   初值

2.  使用这组参数和自变量，预测因变量的值

	-   使用ODE求解器计算（矩阵指数法，刚性，非刚性求解器）

3.  评估因变量预测值和观测值的接近程度

	-   最小二乘法（残差值），最大似然法（似然函数的值）

4.  猜测一组将接近观测值的新参数值

	-   Newton’s Method; Nelder-Mead Simplex Method;

5.  回到步骤2，或者如果我们“足够近(close enough)”则完成

	-   Convergence criterion，收敛准则

参数初值

参数初值的来源多种多样，大体可以如此划分：

-   既往研究获得的值

    -   使用单篇文献中报道的值

    -   对文献数据汇总分析得到的值

    -   之前试验数据分析得到的值

    -   NCA→个体模型→群体模型

-   使用当前数据估算的值

    -   NCA→个体模型→群体模型

    -   网格搜索获得初值

    -   曲线剥离获得初值

    -   可视化调整获得初值

-   从头计算的理论值

    -   由分子结构计算所得的理论值

    -   由其他种属通过异速缩放得到的值

    -   由其他种属IVIVE得到的值

ODE

此部用于计算因变量的预测值，方法由以下几种：

-   已知因变量解析解

    -   将自变量直接带入计算得到

-   未知因变量解析解

    -   使用矩阵指数的方法求解

    -   放弃解析解，使用ODE通过数值逼近的方法求解

        -   LSODE (Livermore Solver)是Phoenix
            Model用于刚性/非刚性常微分方程的求解器

            -   在刚性的情况下，它将雅可比矩阵df/dy视为密集（完整）或带状矩阵，
			并且可以是用户提供的，也可以用差异商在内部近似。它在非刚性情况下使
			用Adams方法（预测校正器），在刚性情况下使用后向分化公式（BDF）方法
			（Gear方法）。产生的线性系统通过直接方法（LU因子/求解）求解。

预测值

预测值就是因变量的预测值，没啥好说的

构建目标函数

构建目标函数的方法由多种，大体可以划分为两种：

-   最小二乘法，目标函数SSR

    -   普通最小二乘

    -   加权最小二乘

    -   扩展最小二乘

-   最大似然法，目标函数-2LL

    -   最大似然
        
		-   类似扩展最小二乘的最大似然
    
	-   限制性最大似然
        
		-   限制性最大似然

目标函数

• 目标函数可用于判断模型的好坏，除了上述提及的两个直接的目标函数SSR与-2LL，还衍生出了基于他俩的一系列其他用于判断模型好坏的信息判据比如：AIC、SBC等等

最小化算法

最小化算法是才是解决非线性问题的核心与灵魂，
也是方法类别最为丰富的地方，可以分为以下这些：

-   搜索法

	-   网格搜索

	-   改良单纯形

-   数值解析法

	-   高斯牛顿

		-   Hartley改良

		-   Levenberg and Hartley改良（猜测是阻尼牛顿）

	-   拟牛顿

		-   DFP

		-   BFGS改良（Phoenix Model使用的方法）

	-   退火法

	-   遗传算法

-   采样法

	-   马尔可夫链蒙特卡罗

退出迭代的条件

退出迭代的条件因软件而已，大致有下以下几种：

-   找到了参数的最小值

    -   这是最理想的解决方案, 在参数空间没有方向,得到一个较低的 SSR/LL

-   两次迭代中参数值的变化在我们的 “公差” 范围

    -   需要的答案的精确程度是多少？

-   两次迭代中SSR/LL 信息判据值在定义的范围中

    -   参数值可能会发生剧烈变化!!!

    -   在这个范围内, SSR/LL "表面" 可能非常平坦

-   达到最大迭代次数

WinNonlin经典模型计算

估计参数的工作的过程是：

1.  猜测一组参数值

    -   网格，曲线剥离，用户提供

2.  使用这组参数和自变量，预测因变量的值

    -   差分法求导，或者直接试用微分方程（信息不足）

3.  评估因变量预测值和观测值的接近程度

    -   最小二乘法（残差值）

4.  猜测一组将接近观测值的新参数值

    -   高斯牛顿

        -   Hartley改良

        -   Levenberg and Hartley改良（猜测是阻尼牛顿）

    -   搜索法

        -   改良单纯形

5.  回到步骤2，或者如果我们“足够近(close enough)”则完成

    -   残差平方和的相对变化小于收敛标准时

    -   达到最大迭代次数

Phoenix Model个体模型计算

估计参数的工作的过程是：

1.  猜测一组参数值

    -   用户提供，可视化初值估计工具

2.  使用这组参数和自变量，预测因变量的值

    -   矩阵法，LSODE求解器

3.  评估因变量预测值和观测值的接近程度

    -   最大似然法

4.  猜测一组将接近观测值的新参数值

    -   拟牛顿,BFGS改良（Phoenix Model使用的方法）

5.  回到步骤2，或者如果我们“足够近(close enough)”则完成

    -   找到了参数的最小值

    -   两次迭代中参数值的变化在我们的 “公差” 范围

    -   两次迭代中SSR/LL 信息判据值在定义的范围中

    -   达到最大迭代次数

Phoenix Model群体模型计算

估计参数的工作的过程是：

1.  猜测一组参数值

    -   用户提供，可视化初值估计工具

2.  使用这组参数和自变量，预测因变量的值

    -   矩阵法，LSODE求解器

3.  评估因变量预测值和观测值的接近程度

    -   最大似然法

        -   FO（在eta的均值处（先验）泰勒展开残差项的积分）

        -   FOCE（在贝叶斯期望最大处泰勒展开残差项的积分）

        -   拉普拉斯（使用拉普拉斯变换的方法直接对残差项的积分进行近似）

        -   QRPEM（待补充）

4.  猜测一组将接近观测值的新参数值

    -   拟牛顿,BFGS改良（Phoenix Model使用的方法）

    -   EM法

5.  回到步骤2，或者如果我们“足够近(close enough)”则完成

    -   找到了参数的最小值

    -   两次迭代中参数值的变化在我们的 “公差” 范围

    -   两次迭代中SSR/LL 信息判据值在定义的范围中

    -   达到最大迭代次数