最小化目标函数算法之直接矩阵求解最小二乘
付永超 / 2019-06-21
我准备开一个新坑介绍一系列最小化目标函数的计算方法,这是本系列的第一篇。
本文介绍一个通过矩阵直接求解最小二乘问题的一个案例,这种计算方法其实不应该被归类到“最小化目标函数”这种方法中,因为这种方根本无需计算目标函数,是通过求解析解的方法解决最小二乘问题,后续的方法都是求数值解的方法,但是该方法确实是一种非常关键且基础的求解最小而成问题的方法,所以首先介绍与实施,该案例使用的数据也会在后续案例中持续使用。
1.使用的数据:
| ID | time | conc |
|---|---|---|
| 1 | 0.5 | 5.95432 |
| 1 | 1 | 5.35306 |
| 1 | 1.5 | 5.03 |
| 1 | 2 | 4.78 |
| 1 | 2.5 | 4.39 |
| 1 | 3 | 3.68 |
| 1 | 4 | 3.2 |
| 1 | 5 | 2.55 |
| 1 | 6 | 2.03 |
| 1 | 8 | 1.28 |
| 1 | 12 | 0.552 |
| 1 | 14 | 0.321 |
1.1数据所对应的散点图:
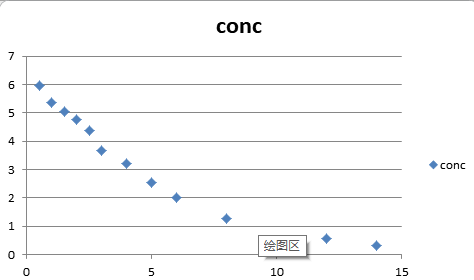
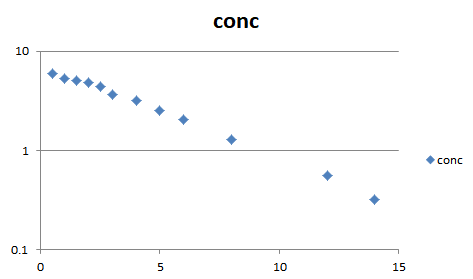
2.案例演示所使用的软件:
Excel2010
3.理论基础:
线性模型可以写为下列形式:
\[ C_{i} = \theta_{0} + \theta_{1} X_{i} + e_{i} \]
\[ C = \theta + \theta X + e_{i} \]
更一般的可以写为下列形式:
\[ C = X\theta + e \]
其中:
C是n*1的观测向量(因变量)
X是n*p的自变量矩阵,又叫设计矩阵
θ是p*1的未知的参数向量
e是n*1的随机误差向量,假设e~N(0,σ^2)
n是观测值得个数
p是未知参数的个数
观测向量(因变量):
\[ C = \begin{pmatrix} C_{1} \\ C_{2} \\ \vdots \\ C_{n} \\ \end{pmatrix} \]
自变量矩阵:
\[ X = \begin{pmatrix} 1 & x_{1} \\ 1 & x_{2} \\ \vdots & \vdots \\ 1 & x_{n} \\ \end{pmatrix} \]
\[ \theta = \begin{pmatrix} \theta_{0} \\ \theta_{1} \\ \end{pmatrix} \]
函数关系:
\[ \begin{pmatrix} C_{1} \\ C_{2} \\ \vdots \\ C_{n} \\ \end{pmatrix} = \begin{pmatrix} 1 & x_{1} \\ 1 & x_{2} \\ \vdots & \vdots \\ 1 & x_{n} \\ \end{pmatrix} \bullet \begin{pmatrix} \theta_{0} \\ \theta_{1} \\ \end{pmatrix} = \begin{pmatrix} \theta_{0} + \theta_{1} \bullet x_{1} \\ \theta_{0} + \theta_{1} \bullet x_{2} \\ \vdots \\ \theta_{0} + \theta_{1} \bullet x_{n} \\ \end{pmatrix} \]
求解参数θ估计值的最基本方法是最小二乘法,其思想是在θ的真值处应使观测值与预测值差值的平方和最小:
\[ \sum_{}^{}e_{i}^{2} = \left( C - \text{Xθ} \right)^{2} \]
\[ {= C^{2} - 2\theta^{'}X^{'}C + \left( \text{Xθ} \right)^{2}} \]
\[ {= C^{'}C - 2\theta^{'}X^{'}C + \theta^{'}X^{'}\text{Xθ}} \]
因为\(\sum_{}^{}e_{i}^{2} = C^{'}C - 2\theta^{'}X^{'}C + \theta^{'}X^{'}\text{Xθ}\)函数在最小值处,其相对与θ的导数为零,
所以
\[ \frac{\partial\sum_{}^{}e_{i}^{2}}{\partial\theta} = 0 \]
\[ -2X^{'}C + 2X^{'}\text{Xθ} = 0 \]
\[ X^{'}C = X^{'}\text{Xθ} \]
\[ \theta{= \left( X^{'}X \right)}^{- 1}X^{'}C \]
方差与协方差矩阵可以被顺便求解出来:
\[ {\hat{\sigma}}^{2} = \frac{\text{WRSS}}{\left( N - P \right)} = \frac{\sum_{}^{}{W_{i}\left( C_{i} - {\hat{C}}_{i} \right)}^{2}}{\left( N - P \right)} \]
其中\({\hat{C}}_{i} = f\left( X,\hat{\theta} \right)\),Wi是权重
\[ \text{Var}\left( \hat{C} \right) = \left( X^{'}X \right)^{- 1}{\hat{\sigma}}^{2} \]
4.实例计算:
4.1使用的模型:
此处直接对原始数据求解线性模型,而使用血管内给药的1房室1级速率消除模型求解它,即使用此模型:C=θ0+θ1*time+e
也可写为:C=θ*X+e
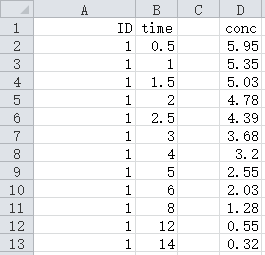
将数据如图所示的写入Excel工作,这样就可以得到设计矩阵(自变量矩阵,下同)与观测向量
4.2设计矩阵X=A2:B13,
4.3观测向量C=D2:D13,
4.4计算参数向量θ:
4.4.1构造设计矩阵X的转置X'
复制A2:B13单元格,鼠标右键单击B15单元格,选择“选择性粘贴”子菜单,勾选其中的“转置(E)”选项,然后确定,这样就得到了设计矩阵X的转置矩阵X'
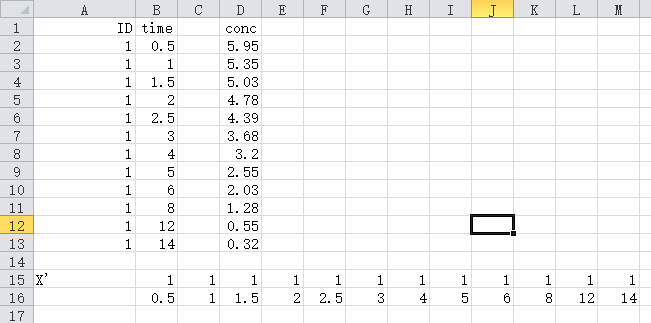
设计矩阵的转置X'=B15:M16
4.4.2计算X'X
选中B18:C19这四个单元格,然后在输入=MMULT(B15:M16,A2:B13),之后在键盘上同时按下“Ctrl”键和“Shift”键不放,再按下“回车”键完成数组构建。
(小提示:
1.MMULT()是Excel中的矩阵乘法公式,
2.矩阵的乘法有先后顺序之分,右侧的矩阵依次乘左边的矩阵,所以顺序部分反
3.同时按下“Ctrl”键+“Shift”键+“回车”键是Excel中数组公式的输入方式,这种方式输入公式后,选中其中的单元格可以看到公式外自动添加了大括号,
3.要对包含同一个数组公式的单元格进行修改,必须选中所有的包含同一个数组公式的单元进行修改,无法单独的更改其中1个单元格)
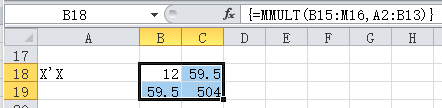
X'X=B18:C19
4.4.3计算X'X的逆矩阵(X'X)-1
选中B21:C22这四个单元格,然后在输入=MINVERSE(B18:C19),之后同时按下“Ctrl”键+“Shift”键+“回车”键完成数组构建。
(小提示:MINVERSE()是Excel中的求逆矩阵的公式)
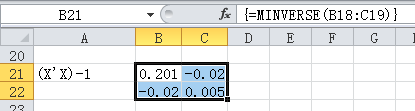
X'X的逆矩阵(X'X)-1=B21:C22
4.4.4计算(X'X)-1*X'
选中B24:M25这24个单元格,然后在输入=MMULT(B21:C22,B15:M16),之后同时按下“Ctrl”键+“Shift”键+“回车”键完成数组构建。

(X'X)-1*X'=B24:M25
4.4.5计算(X'X)-1*X'*C
选中B27:C28这2个单元格,然后在输入=MMULT(B24:M25,D2:D13),之后同时按下“Ctrl”键+“Shift”键+“回车”键完成数组构建。
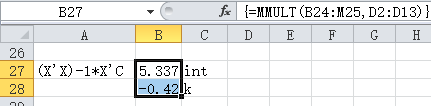
(X'X)-1*X'*C=B27:C28
4.5结果解读
这样便求算出了参数矩阵θ=B27:C28,其中截距=B27=5.337,斜率=C28=-0.419
4.6计算RSS
在得到截距与斜率这两个参数后,求可以计算出因变量C的预测值Pre,观测与预测的残差Res,残差平方和RSS
Pre:在E2单元格输入=$B$27+$B$28*B2,然后下拉填充至E13单元格
Res:在F2单元格输入=D2-E2,然后下拉填充至F13单元格
RSS:在G2单元格输入=SUMSQ(F2:F13)
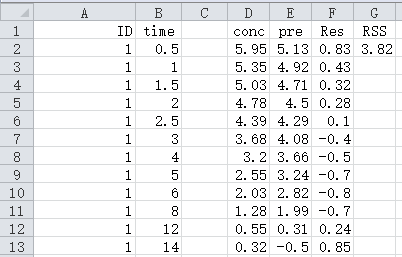
RSS=G2
4.7计算协方差矩阵Var(C)
选中F21这1个单元格,然后在输入=B21*$G$2,之后通过拖拽填充的方式填充F22,G21,G22单元格。
(小提示:这里因为是常数(RSS)与矩阵相乘所以不需要使用矩阵乘法公式)
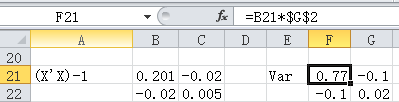
Var(C)=F21:G22
5.小结:
以上就是一个完整的使用Excel逐步手工通过矩阵求解线性模型最小二乘问题的完整步骤,理解上述步骤对之后掌握其他方法的基础!
