文献名字：Importance of Shrinkage in Empirical Bayes Estimates for Diagnostics: Problems and Solutions

中文直译：诊断经验贝叶斯估计中收缩的重要性：问题与解决方案

网址连接：https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2758126/

PMID: 19649712

名词解释：

收缩"Shrinkage"，是指在包含随机效应的模型中，由模型可以估计得到随机效应的标准偏差值(ω)，另外由模型和观测值还可通过贝叶斯反馈（Empirical Bayes (“post hoc”) estimates (EBEs)）估计得到具体的每一个个体(i)的个体参数的值ηEBE，然后对所有ηi进行描述性统计可以得到SD(η)，则该随机效应的参数值的收缩值计算公式为：

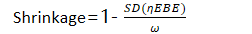
收缩值可以反应当前数据所包含的信息是否足以支持对于该随机效应估计，越小越好，当收缩值过大时，提示当前数据并不足以估计该随机效应，有该随机效应所预测的EBE个体值也是失真的，不能发挥诊断和协变量搜索的作用。

一般：

• Shrinkage的值在0~1之间，
• 当Shrinkage取负值时，则提示经验贝叶斯估计的参数分布方差比估计的方差值大，模型对该随机效应的方差指定可能存在错误。
• 越接近0表示收缩值越好，没有金标准的接受标准，但一般认为小于20~30%以下是可以接受的，
• 当高于30%则提示当前的数据不足以支持估计该参数的个体间变异，与之相关的诊断图表不能够正确的显示诊断信息，不能用用于诊断；较大的收缩值并不能有用于指示当前的模型是否被错误指定，即使是正确的模型依然可能会遇到收缩值较大的情况。
• 当收缩值较大时，表示经验贝叶斯估计的个体参数的分布方差比模型估计的方差小，此时的个体参数不能很好的符合模型估计的分布，而表现出更加集中的分布，极端情况，当EBEs估计的参数方差为0即，Shrinkage=1时，EBEs估计的参数都是群体典型值。
• 当该随机效应估计得到的方差很小，收缩值很大时，提示当前的数据不足以估计该参数的随机效应，可取消对改参数的随机效应的估计，即不估计改参数的随机效应。
• 对于个体内残差的收缩值计算公式也是采用上述公式，但有时会做一些变形：

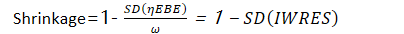
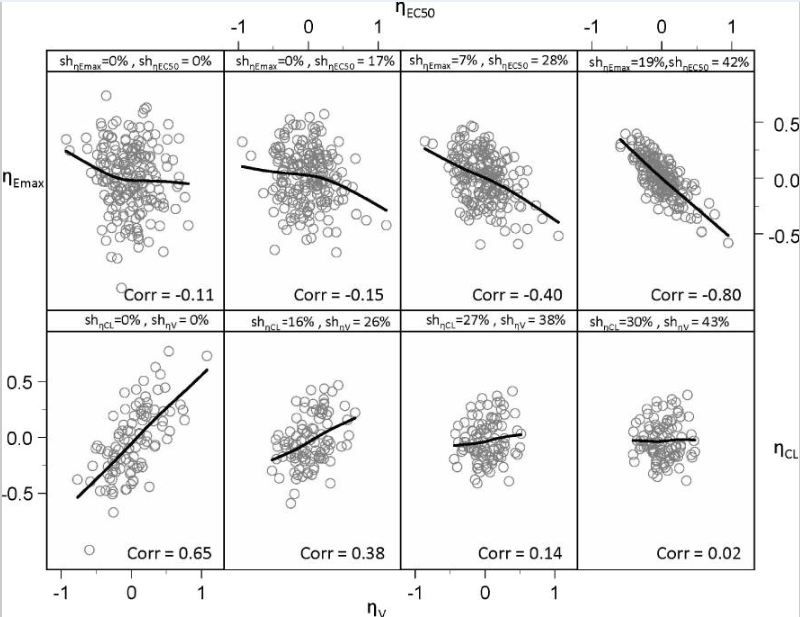
文献综述的图表：

Eta对Eta相关性图表，在不同收缩值情况下的展示。

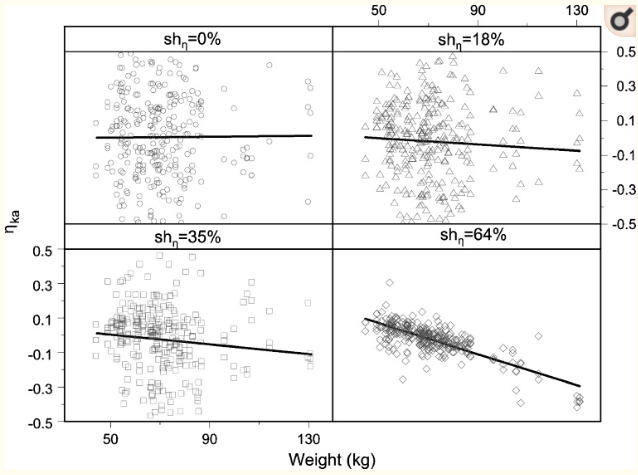
Eta对协变量图，无相关在高收缩情况下出现相关。