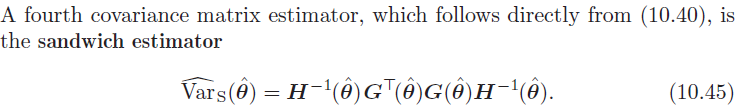标准误步骤($COV)的计算方法
付永超 / 2019-10-22
R、S矩阵^[https://mp.weixin.qq.com/s/g7C3RwRD14wEEi8MTXlTnw]
R矩阵
R矩阵是目标函数在最终参数估计值处的二阶导数矩阵(即黑塞Hessian矩阵,大名鼎鼎的费雪信息矩阵就是负的黑塞矩阵)。它刻画的是目标函数空间在最终参数估计处的曲率。曲率越大,参数估计的精确度越高。
S矩阵
S矩阵是各个个体的目标函数在最终参数估计处的梯度向量(一阶导数)与其本身转置向量乘积的和(梯度外积估计量,outer-product-of-the-gradient)。
1)S矩阵只涉及一阶求导,所以数值计算起来相对容易。如果$COV的警示中出现关于S矩阵的问题,模型就很大可能存在问题。
2)S矩阵是R 矩阵的近似,在随机效应服从正态分布的前提下,随着样本量增大,两者趋于一致。
理解:
R矩阵即Hessian矩阵,原函数的二阶导数,
S矩阵即雅可比矩阵与自身转置的乘积,雅可比矩阵原函数的一阶导数,高斯牛顿法中,使用J-1J近似Hessian矩阵。
协方差矩阵的计算:
最大似然法计算协方差矩阵的方法有4种^[这些结论概念参考自《计量经济理论与方法》,译者沈根祥,343页, 第十章 极大似然方法,10.4 ML估计量的协方差矩阵,节中的介绍],
1.基于Hessian矩阵计算,-H-1
NONMEM
在MATRIX=R的情况下,输出方差-协方差矩阵为2R-1;
以下计算类似,参考资料中估计的是LL(Log likelihood ),NONMEM估计的是-2LL(-2Log likelihood ),所以-2 (-H-1)=2H-1。
NLME
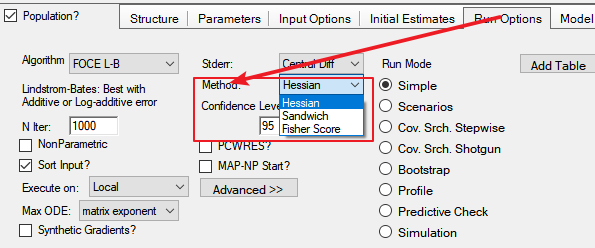
猜测,在将“Stderr Method(标准误计算方法)”设定为“Hessian(黑森)”的情况下,采用该方法完成标准误的计算。(下图为Phoenix8.1中的截图)
2.基于费雪(Fisher)信息矩阵计算,I-1
3.基于梯度矩阵(雅可比矩阵)计算,(GtG)-1
NONMEM
而在MATRIX=S的情况下输出方差-协方差矩阵为4S-1。
参考资料中估计的是LL(Log likelihood ),NONMEM估计的是-2LL(-2Log likelihood ),(瞎猜下)所以(-2*-2)(GtG)-1=4(GtG)-1。
NLME
Phoenix拥有一个以F开头的第三种标准误计算方法“Fisher Score(费雪评分)”,我不知道该方法具体指的怎样的计算方法,但猜测可能是采用费雪信息矩阵计算,但暂且也归类到基于梯度矩阵计算的方法中。
认为是第二种方法的佐证:
https://en.wikipedia.org/wiki/Scoring_algorithm
认为是第三种方法的佐证:
https://support.certara.com/forums/topic/1350-what-does-fisher-score-mean/
Certara官方回复说“Fisher Score(费雪评分)”是指与NONMEM一样的基于S矩阵的算法。
4.基于三明治矩阵计算,H-1GtGH-1
NONMEM
在默认设定下,NONMEM计算的方差-协方差矩阵是 R-1SR-1(被形象的称为三明治矩阵)。在偏离正态分布假设的情况下,三明治矩阵更鲁棒(robust,健壮)更能反映真实的方差-协方差矩阵,这也是它被设定为NONMEM默认输出的原因。在$COV模块下,也提供了其他方差-协方差矩阵的计算方法。
参考资料中估计的是LL(Log likelihood ),NONMEM估计的是-2LL(-2Log likelihood ),所以((-2)(4-1)(-2))H-1GtGH-1=H-1GtGH-1。
NLME
Phoenix8.2默认情况下也是采用Sandwich算法。
参考资料:


中文翻译版把10.45的公式写错了,附上英文原版的该公式。