半年前在阅读PKPD杂志的在线版时阅读到了其中一篇文章《Challenge model of TNFα turnover at varying LPS and drug provocations》，这是一个涉及到3种物质的一篇PKPD分析文章，文献数据的来源来自于“Grünenthal GmbH”，一家德国公司，中文名格兰泰，他家公司曾有一款药物登上过“初中/高中”的课本，非常著名~~，另外该公司的数据所对应的试验是在睿智化学公司进行的，我以前所在的公司。。

扯远了，我们回归正题关注下该文献本身的内容。

该研究主要完成了以下工作：

1.提出了一个新的机制性的解释LPS（脂多糖）诱导的TNF-α（肿瘤坏死因子α）的“疾病模型”，我不太确定在这里使用“疾病模型”是否恰当，或许也可以说为是一个新的机制性的解释LPS（脂多糖）诱导的TNF-α（肿瘤坏死因子α）的PKPD模型（药物代谢动力学于药物效应动力学模型）。

• 该模型使用一房室模型描述LPS在体内的药动学行为

• 使用周转室模型描述TNF-α这种内源性物质的药动学行为，但与典型的周转室模型不同，他认为

  • TNF-α也有一个分布的过程，并使用2房室模型描述TNF-α的分布。
  • TNF-α在初始时刻为零，生成速度由LPS影响。

• LPS与TNF-α之间通过转移室模型进行链接，

  • 转移室模型由3个房室，
  • LPS的浓度通过Emax模型（激活、无基线、非S形，Emax=1）影响转移室中第一个房室中的输入速率，
  • 转移室模型的最后一个房室中的量通过一个Emax模型（激活、无基线、S形）影响TNF-α的生成。

2.描述了该申办方自己的一个化合物“A”的药动学特征。

• 一级速率吸收一房室非线性消除模型。

3.描述了化合物“A”的浓度如何影响TNF-α的值。

• 化合物“A”的浓度度通过Emax模型（抑制、有基线、非S形，E0=1）影响TNF-α的生成。

4.文章的最后附上了他关于参数名感性分析，模型参数可识别性分析的所使用的程序。

我想做什么？

看到该模型型后我想尝试在Phoenix Model中重现该模型。

我目前已经使用图形化模型编辑工具的方法与PML语言重现了不包含个体间变异的该模型（误差模型我暂时都是用的加和型误差）。

看到该模型的结构示意图：

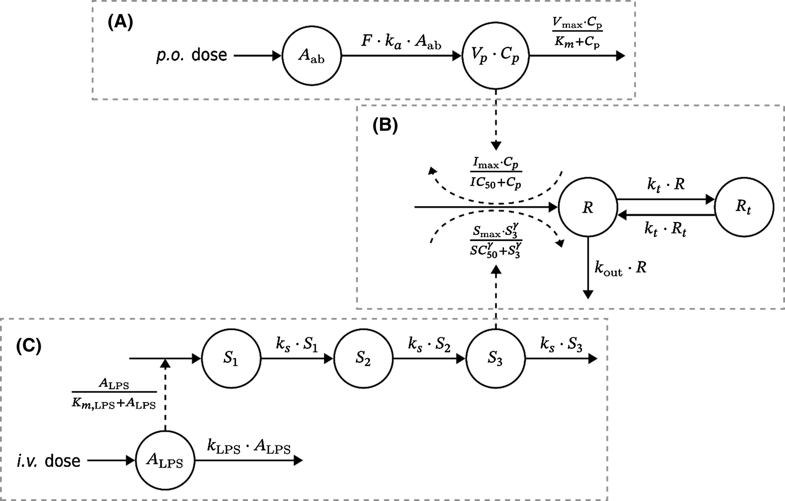
就然人非常有在Phoenix中使用图形化模型编辑工具是实现它的冲动，我尝试去做了，但是失败了：

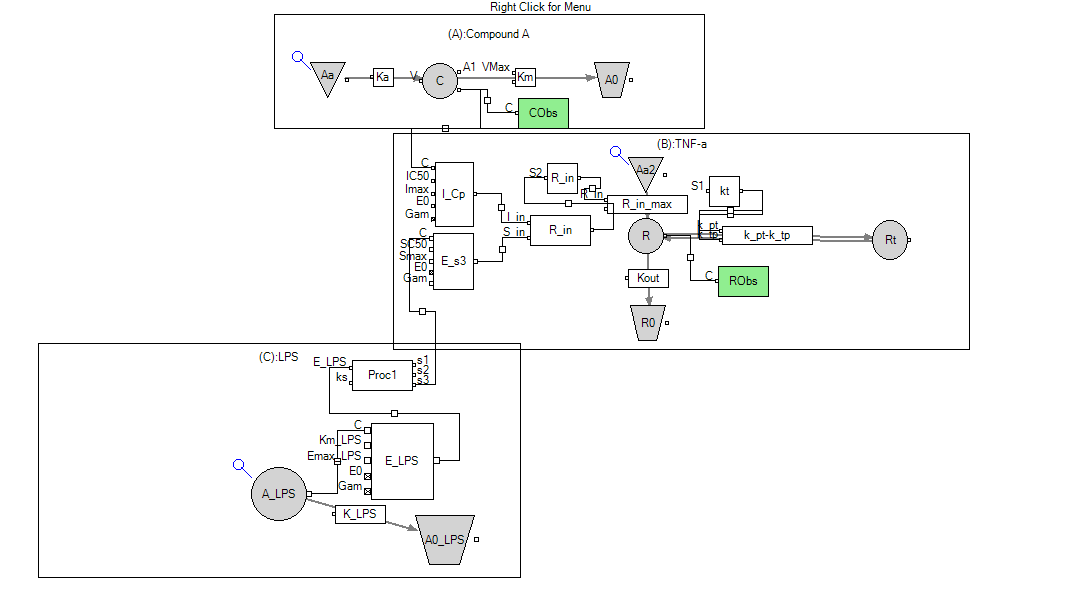
看起来该模型似乎是完全重现了，但在这里我做了一个额外的近似，Phoenix的图形化建模型方式并不能很好的表达出0级速率，所以我在这里将R（对应的时TNF-α的浓度）的吸收室到中央室的转运设置为非线性的过程，然后将Km舍得极小，Vmax设的极大已近似一个0级过程，然后将LPS与A对TNF-α的影响连接到Vmax这个参数上。

另外在执行该模型时需将ODE（常微分方程求解器）切换到**stiff（刚性）**模式，这样才能正常计算，否则无法计算。

为了避免该近似，我也尝试通过在图形化模型编辑工具添加“Procedure（程序语句）”组件，在其中写入TNF-α的微分方程来解决该问题，如下图：

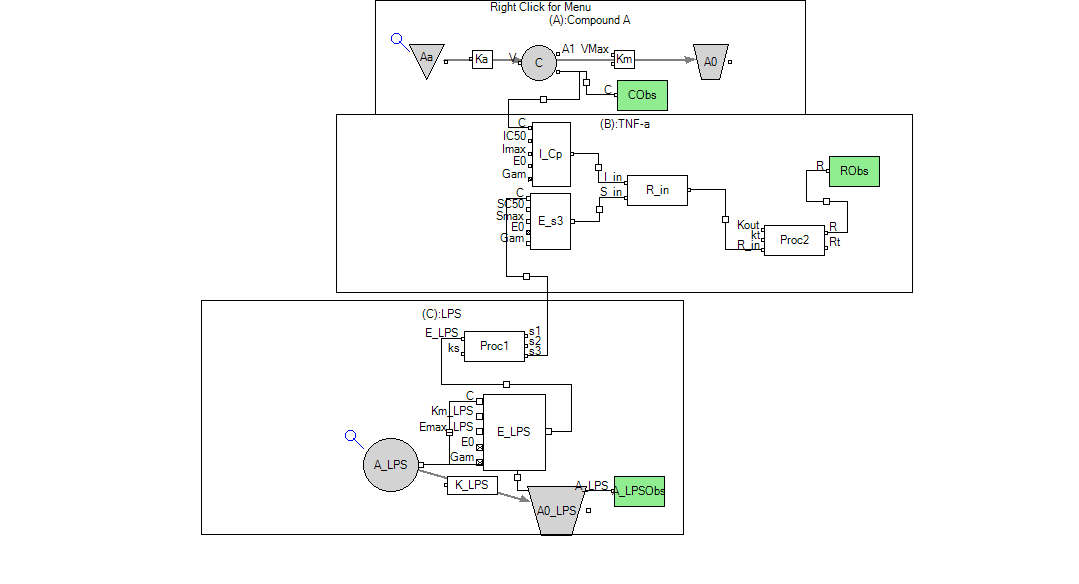
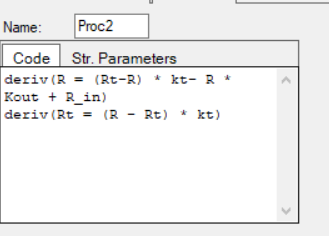
通过这种“图形化”+“代码”的方式可以完美的实现该模型。

3.最后我也使用代码的方式实现了该模型，一通的折腾下来，最后发现其实还是代码的方式最简单直接。。。：

test(){
	#A
	deriv(A1 = - (VMax * C / (C + Km)) + (Aa * Ka))
	urinecpt(A0 = (VMax * C / (C + Km)))
	deriv(Aa = - (Aa * Ka))
	C = A1 / V
	
	#LPS
	deriv(A_LPS = - (A_LPS * K_LPS))
	urinecpt(A0_LPS = (A_LPS * K_LPS))
	deriv(s1 = ks *((A_LPS / (Km_LPS + A_LPS))-s1))
	deriv(s2 = ks * (s1-s2))
	deriv(s3 = ks * (s2-s3))
	
	#TNF-a
	deriv(R = E_s3*I_Cp -R*Kout +(Rt-R)*kt)
	E_s3 = (Smax * s3^Gam / (SC50^Gam + s3^Gam))
	I_Cp = 1 - (Imax * C) / (IC50 + C)
	deriv(Rt = (R-Rt)*kt)
	
	#Dose
	dosepoint(Aa)
	dosepoint(A_LPS,tlag = 2)
	#dosepoint(R)
	#sequence{R = 0}
	
	#Obs
	observe(CObs = C + CEps)
	error(CEps = 1)
	
	observe(A_LPSObs = A_LPS + A_LPSEps)
	error(A_LPSEps = 1)
	
	observe(RObs = R + REps)
	error(REps = 1)
	
	#Initial
	#A
	V=3.3
	VMax=32.2
	Km=18.2
	Ka=1.72
	
	#LPS
	K_LPS=8.36
	ks=3.28
	Km_LPS=0.0789
	
	#TNF
	Smax=6*10^(5)
	SC50=0.469
	Gam=3.79
	
	Imax=0.675
	IC50=0.0231

	Kout=5.65
	kt=0.419
}

给药方案

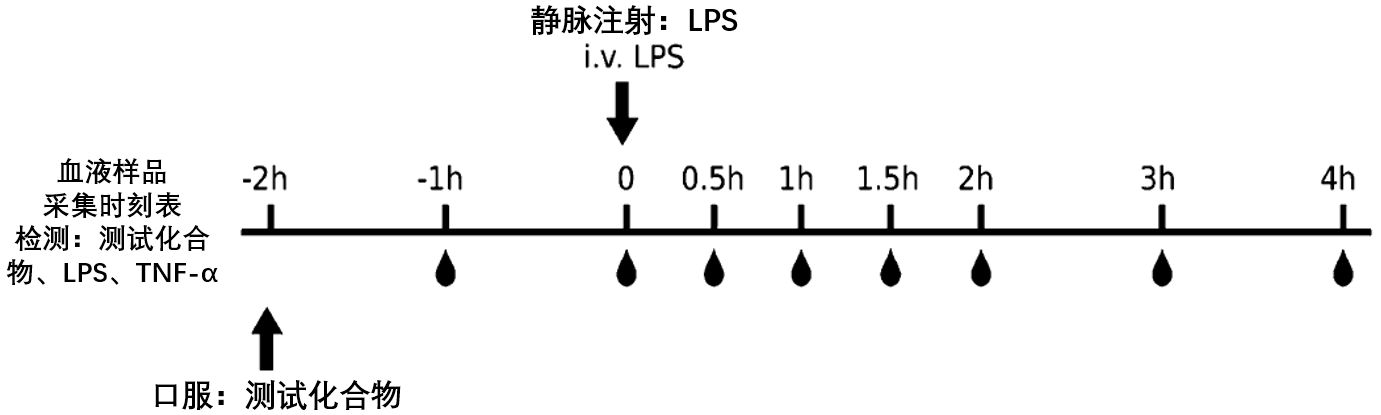
结果：

对文献中提出的场景进行模拟重现，结果如下，

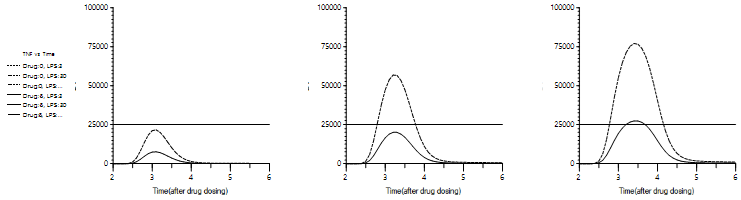
本文所得结果：

上排：不同LPS剂量（3、30、300 µg·kg-1）所产生的TNFα反应对时间图(给与测试化合物后的时间)，实线为同时给予3 mg·kg-1测试化合物，虚线为同时不给予测试化合物。

下排：固定的LPS剂量（30μg·kg-1）所产生的TNFα反应对时间图(给与测试化合物后的时间)，实线为同时给予0.03、0.3和3.0 mg·kg-1测试化合物，虚线为同时不给予测试化合物。

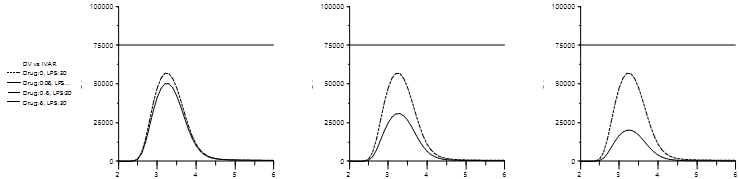
文献原文中的结果：

上排：不同LPS剂量（3、30、300 µg·kg-1）所产生的TNFα反应对时间图(给与LPS后的时间)，实线为同时给予3 mg·kg-1测试化合物，虚线为同时不给予测试化合物。

下排：固定的LPS剂量（30μg·kg-1）所产生的TNFα反应对时间图(给与LPS后的时间)，实线为同时给予0.03、0.3和3.0 mg·kg-1测试化合物，虚线为同时不给予测试化合物。

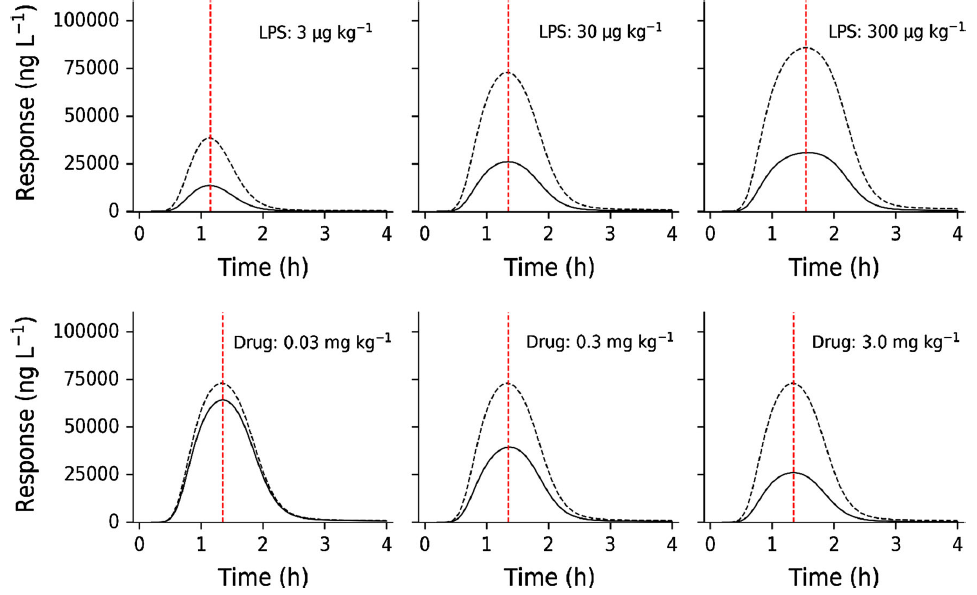
差异：

可以看到，本文得到的结果总体趋势与曲线形状与文献报道的一致，但峰值相对文献偏低，原因未知。