一、前言：

BE数据分析使用的是"线性混合效应模型”，Pop PK使用的是"非线性混合效应模型”，显然"线性混合效应模型"和"非线性混合效应模型"是由关系的，且"非线性混合效应模型"似乎应比"线性混合效应模型"更灵活，那可否使用"非线性混合效应模型"对常见的BE数据进行分析呢？

这个问题一直萦绕在我脑海里，一直在思考怎么实现，这两天有些眉目了，以实现了一些结果，大家一起来欣赏下吧。

二、摘要：

实现了使用Phoenix软件钟用于进行“非线性混合效应模型”建模的操作对象“Phoenix Model”对BE数据的分析，不进行最终的假设检验结果，仅在获取统计模型中的个固定效应与随机效应的估计值，获得其中：对22试验设计的数据分析出的结果与"线性混合效应模型"的最大似然估计结果一致，参数估算值的前5位都是一致的；对于24试验设计的数据，应用“非线性混合效应模型”无法直接获得对应于"线性混合效应模型"结果中的随机效应的方差值，需要额外的手工进行变换与运算，转换所得结果与线性混合效应模型"的最大似然估计结果一致，但仅参数估算值的前3位都是一致的。对比两种模型的结果，固定效应部分一般估计都是一致的，使用“非线性混合效应模型”对随机效应部分的处理较为麻烦，且由于Phoenix对同一事物的观测仅能包含一个随机误差，导致实现2*4对应的模型困难，需额外进行一些假设与转换。

三、作者目的：

该文主要用于帮助作者梳理"线性混合效应模型"和"非线性混合效应模型"的联系，并非用于正式计算BE试验的结果，读者也可自己尝试进行此类的思考与操作，增进对"非线性混合效应模型"的理解，另外本文建模过程用到了群体模型中的IOV变异，也可帮助读者进一步理解IOV。

四、正文：

A、背景：

相关链接：

读者可参阅该文了解2*2试验设计的生物等型试验数据分析中所使用的统计学模型，已及使用Phoenix分析数据后获得结果的解读，

统计学模型：

众所周知，在分析2×2生物等效性试验的数据时，我们需要按照监管机构的要求来进行分析，目前美国FDA使用如下统计学模型：

其中k代表个体，j是时段数，i是排序数；Yijtk为第k个受试者、第i种顺序，在第j个周期、第t种制剂所观测的实验效应；

μ为总的平均效应；Ƴi为顺序的固定效应；Sk(i)为第k个受试对象在第i个顺序中的随机效应；πj为第j个周期的固定效应；σt为第t种制剂的固定效应；εijtk为Yijtk的残差，为随机误差。

大串公式记不住，可以口语化的记为：

Y =平均值+贯序+受试者(贯序)+周期+制剂+个体内变异

所使用的数据：

Phoenix自带的2*2生物等效性数据

B、使用Phoenix的Bioequivalence操作对象对数据进行分析

固定效应的估计值

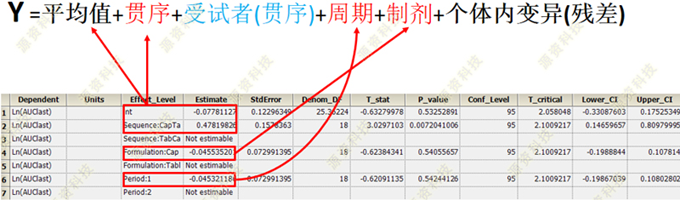
随机效应方差的估计值

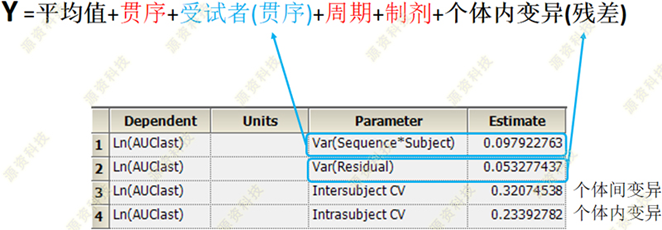
C、使用SPSS的"线性混合效应模型"对数据进行分析（REML）

1.导入数据

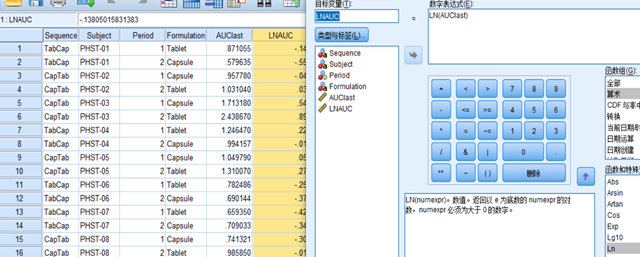
2.计算LN(AUC)

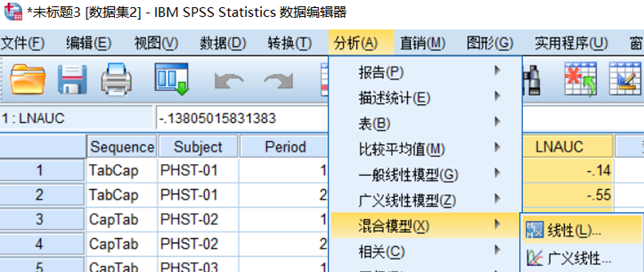
3.发送至线性混合效应模型分析

4.配置“线性混合效应模型”对象

4.1指定

主体：Subject

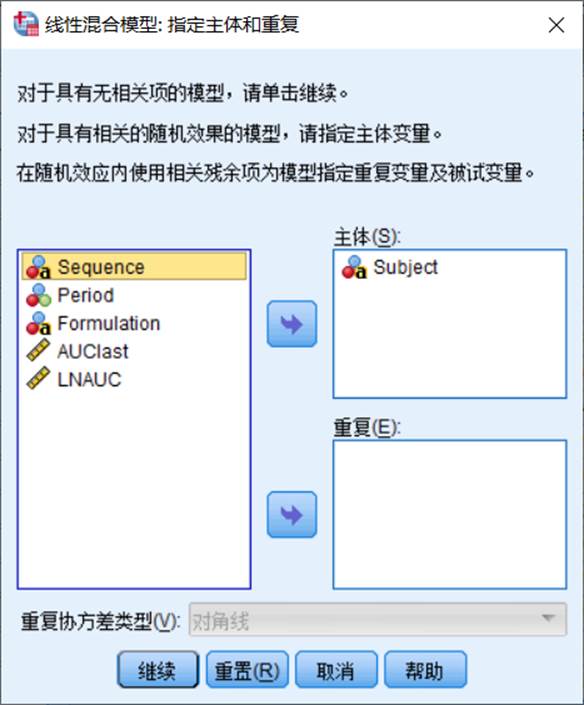
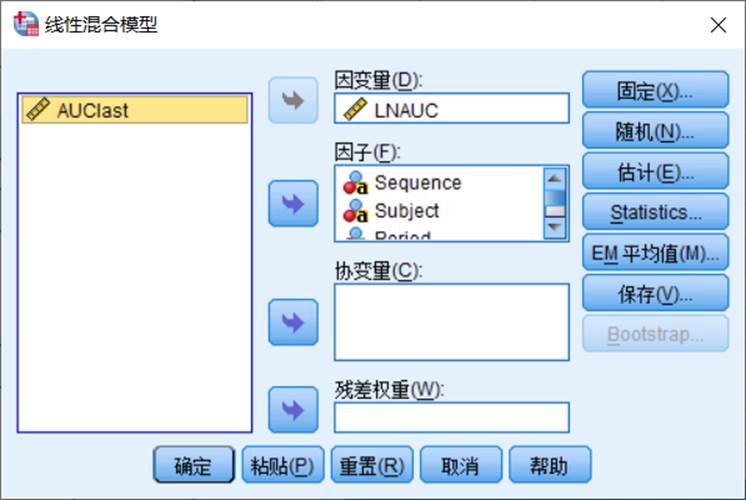
4.2指定

因变量：LNAUC

因子：Sequence，Period，Formulation

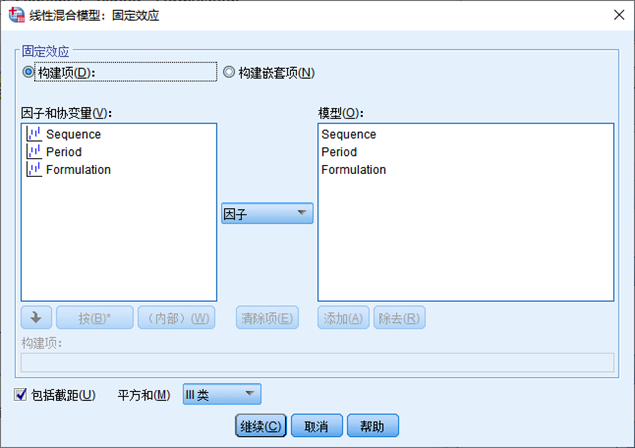
4.3指定固定效应

固定效应：Sequence，Period，Formulation，截距

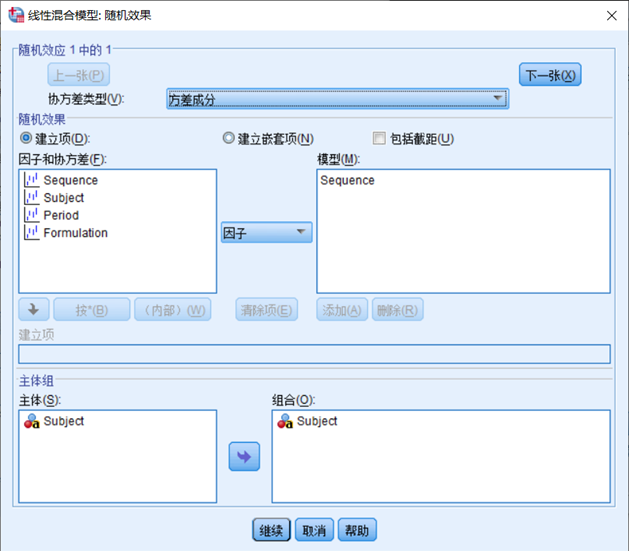
4.4指定随机效应

随机效应分组因素：Sequence

随机效应主体：Subject

随机效应协方差类型：方差成分

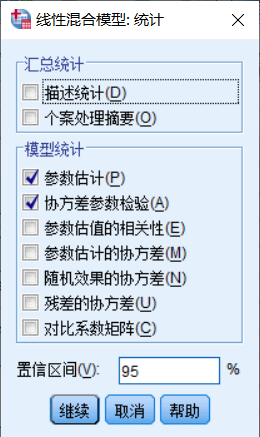
4.5所需统计的结果

勾选：

固定效应的 参数估算值

协方差参数检验

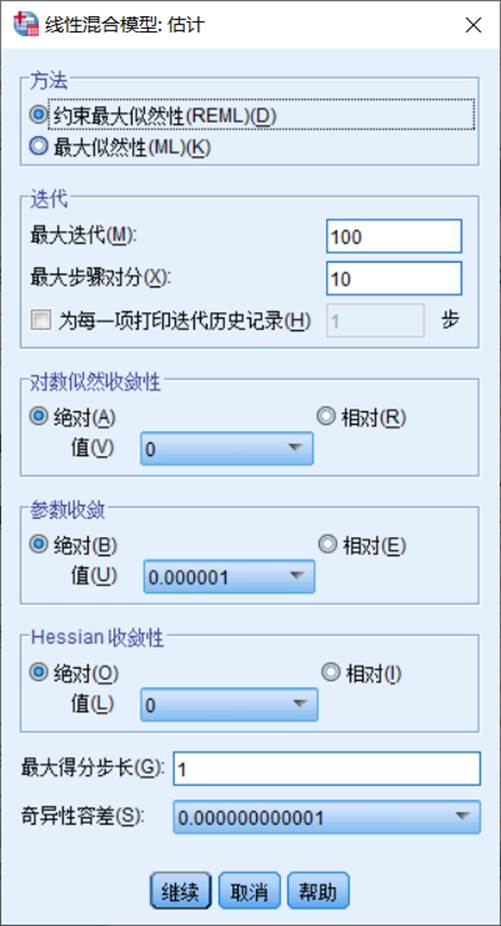
4.6估计

勾选使用“约束最大似然性（REML）”方法

5.执行

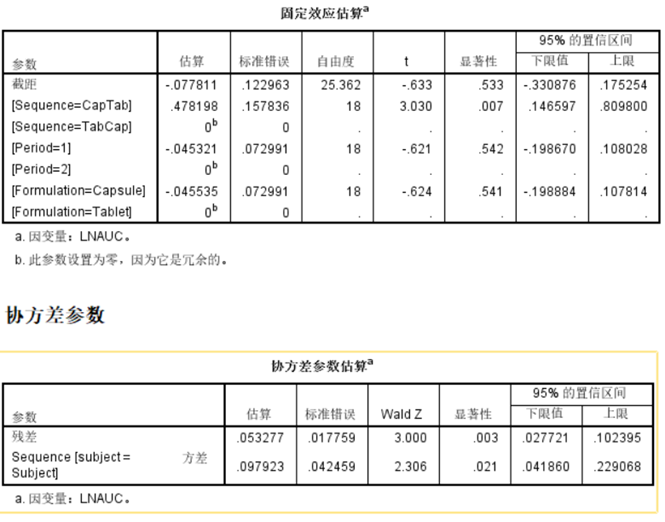
6.结果

D、使用SPSS的"线性混合效应模型"对数据进行分析（ML）

1、与上一节设置的差异

本部份大部分操作与上述一样，仅将“4.6估计”中的方法改为“最大似然型（ML）”

2、结果

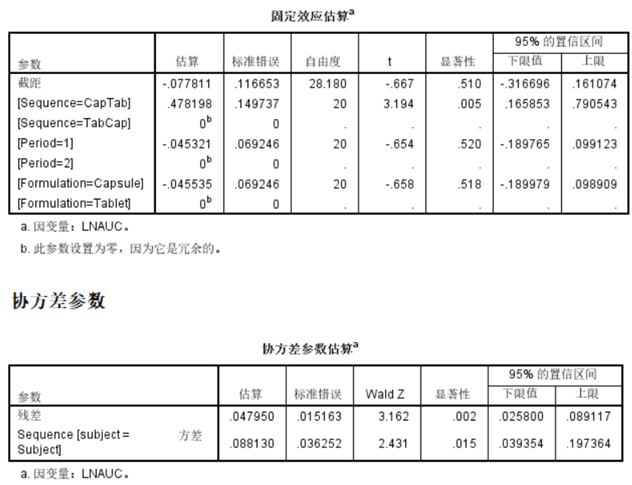
两种方法差异：

读者可自行搜索了解“约束最大似然性（REML）”和“最大似然型（ML）”方法的差异，这里不做详述，两种方法的差异在这里主要是协方差矩阵中随机效应方差的自由度的差异，REML的自由度比ML更小，所以看起来ML方法的随机效应方差更大。

另外，“非线性混合效应模型”一般都采用的是“最大似然型（ML）”的方法而非“约束最大似然性（REML）”所以这里额外使用“最大似然型（ML）”方法计算出一份结果，便于之后与“非线性混合效应模型”的方法比较。

E、使用Phoenix的"Phoenix Model"对数据进行分析（ML，FOCE L-B）

1.数据准备

1.1额外新增一个辅助列

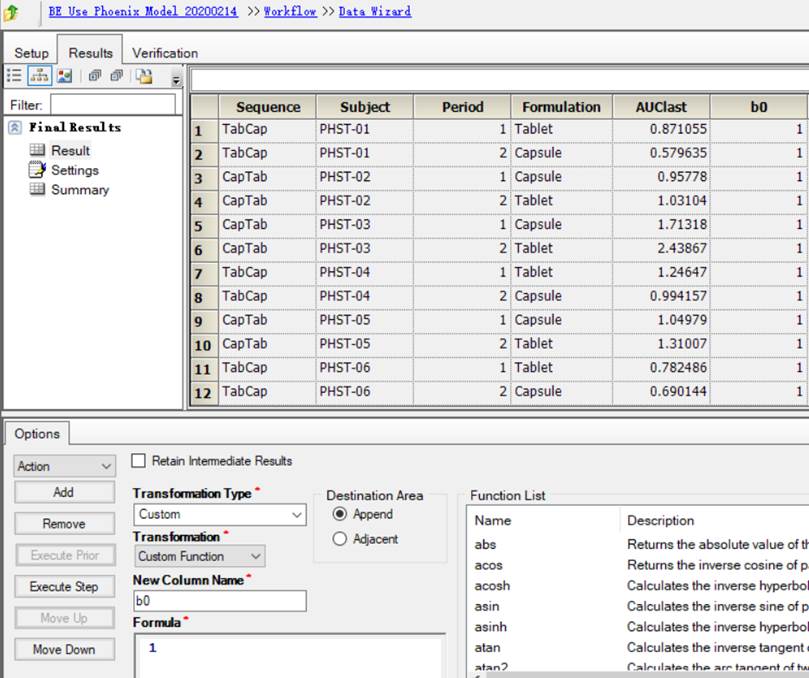
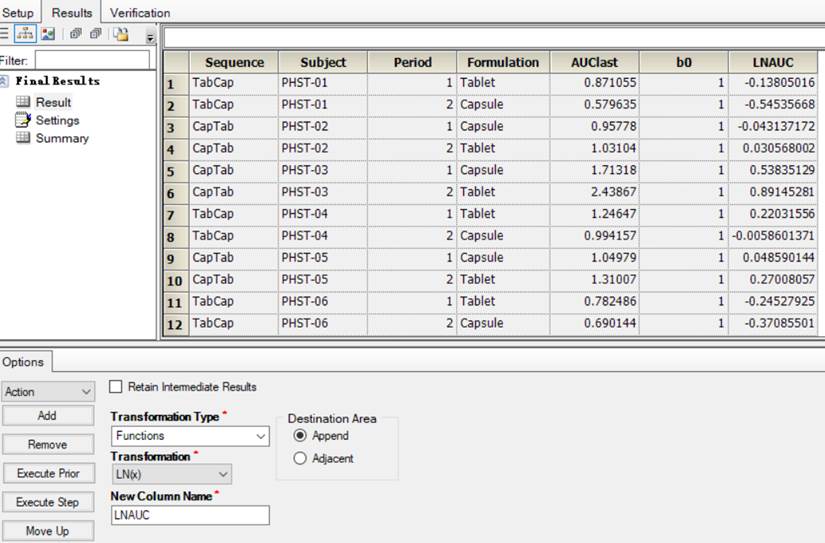
1.2计算LNAUC

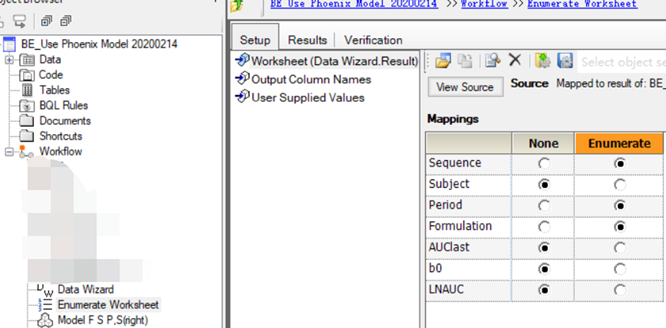
1.3使用“Enumerate（枚举）”对象将分类变量转换为整数

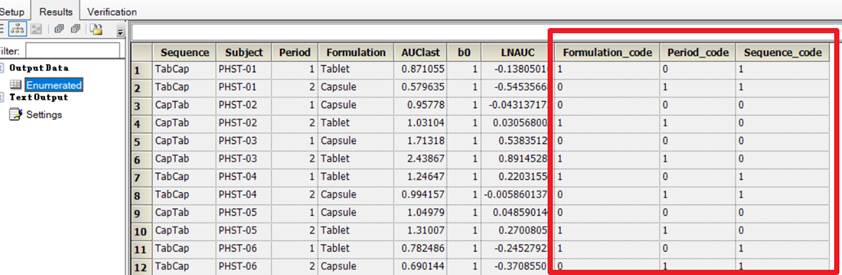
2.Phoenix Model对象的设置

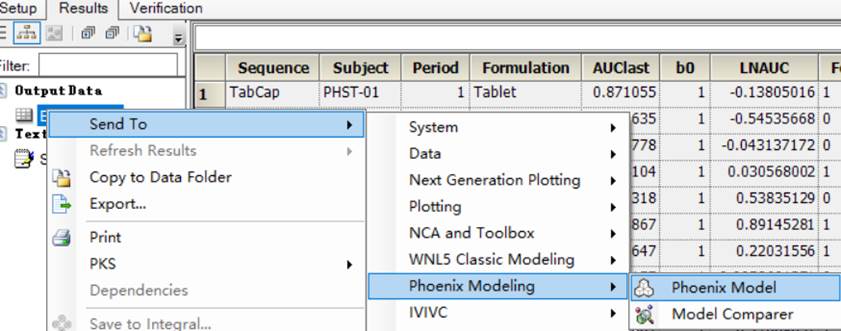
2.1发送至Phoenix Model

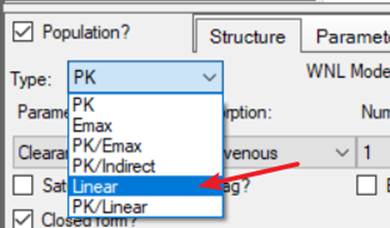
2.2选择模型

将模型类被设定为“Linear”

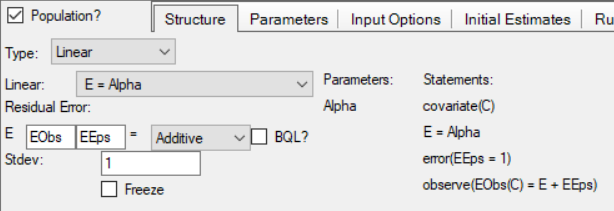
2.3增加协变量

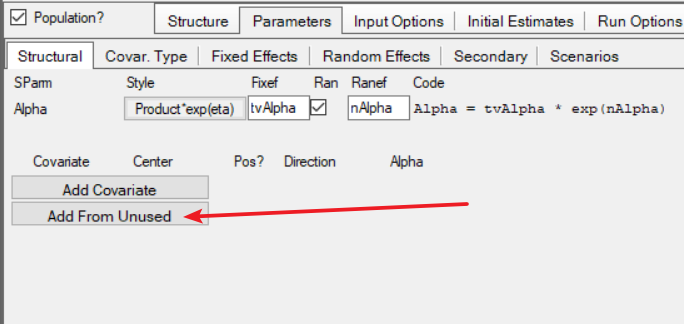
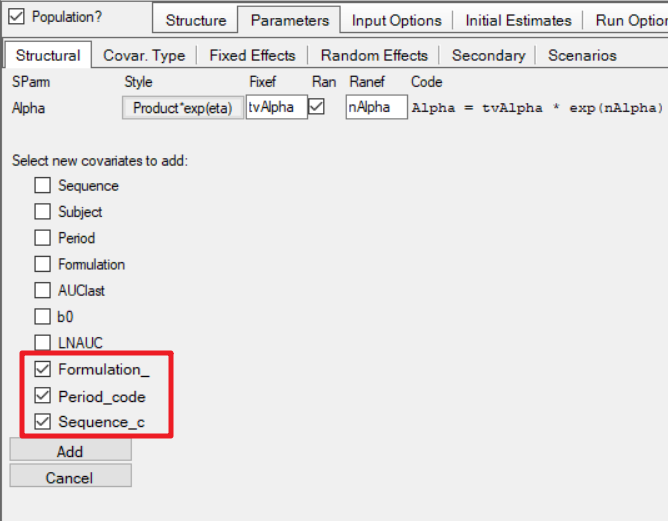
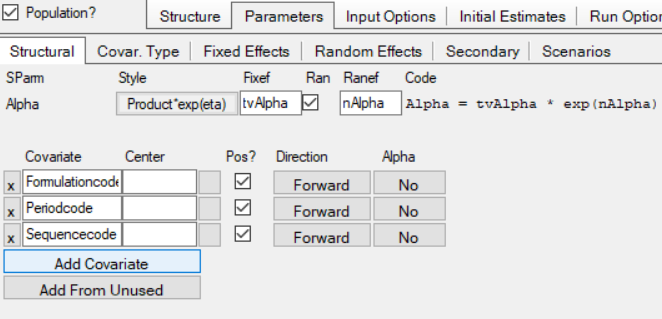
2.4设定协变量类型

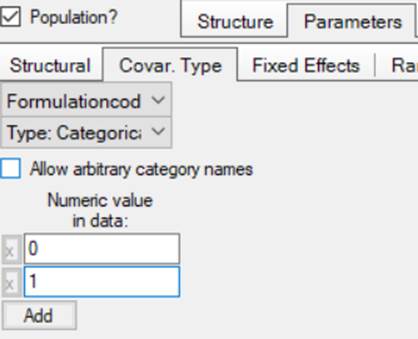
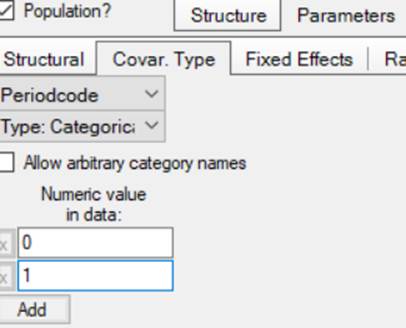
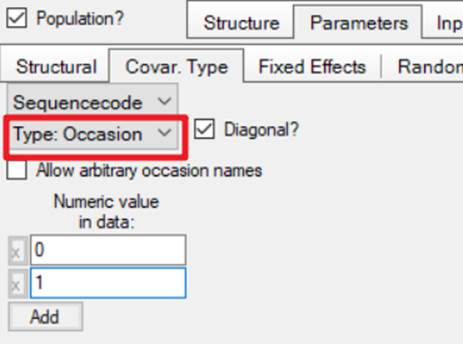
2.5设定参数的统计学模型

2.5.1修改随机效应风格

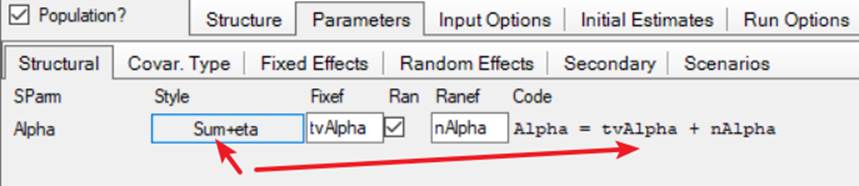
2.5.2移除“Alpha”的随机效应

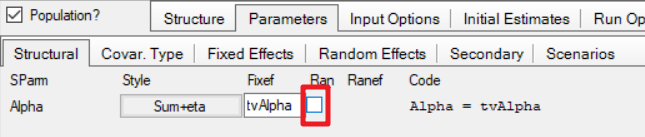
2.5.3将协变量引入模型

2.5.4进行变量映射

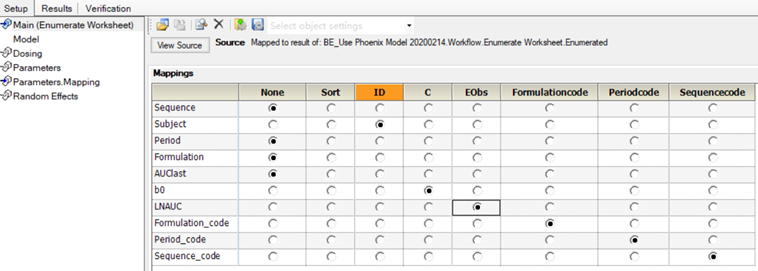
2.6小结

当的模型已经包含了以下部分

固定效应：截距，周期，制剂

随机效应：残差，受试者嵌套在序列中的随机效应

还缺一个固定效应：序列

Phoenix不能直接将一个协变量纳入模型中两次，我们之前已经将“序列”包含在了随机效应中了一次，所以不能直接在将它在纳入固定效应，所以接下来为了纳入将其纳入，我们将模型切换为文本模式进一步修改。

2.7进一步的修改模型

2.7.1将模型编辑方式由内置模型编辑模式切换为文本编辑模式

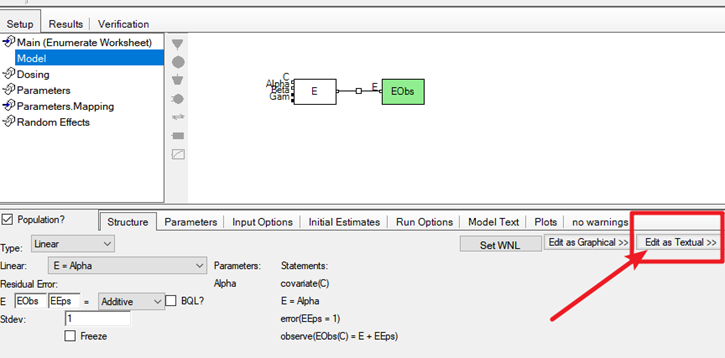
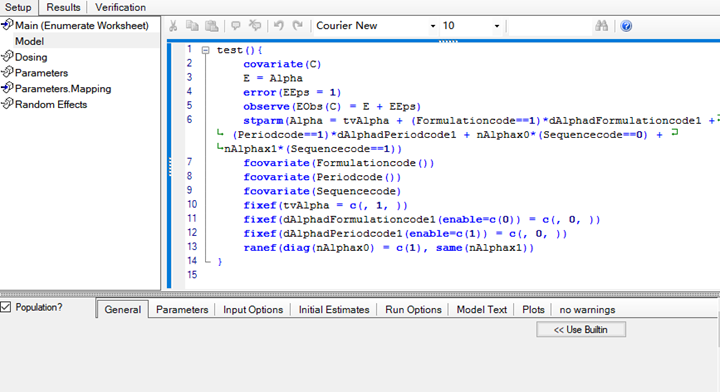
2.7.2当前模型的代码

test(){
covariate(C)
E = Alpha
error(EEps = 1)
observe(EObs(C) = E + EEps)
stparm(Alpha = tvAlpha + (Formulationcode==1)*dAlphadFormulationcode1 + (Periodcode==1)*dAlphadPeriodcode1 + nAlphax0*(Sequencecode==0) + nAlphax1*(Sequencecode==1))
fcovariate(Formulationcode())
fcovariate(Periodcode())
fcovariate(Sequencecode)
fixef(tvAlpha = c(, 1, ))
fixef(dAlphadFormulationcode1(enable=c(0)) = c(, 0, ))
fixef(dAlphadPeriodcode1(enable=c(1)) = c(, 0, ))
ranef(diag(nAlphax0) = c(1), same(nAlphax1))
}

2.7.2模型代码修改

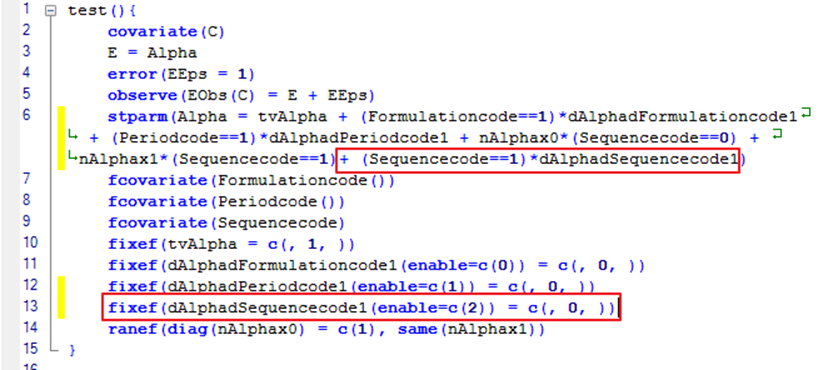
test(){
covariate(C)
E = Alpha
error(EEps = 1)
observe(EObs(C) = E + EEps)
stparm(Alpha = tvAlpha + (Formulationcode==1)*dAlphadFormulationcode1 + (Periodcode==1)*dAlphadPeriodcode1 + nAlphax0*(Sequencecode==0) + nAlphax1*(Sequencecode==1)+ (Sequencecode==1)*dAlphadSequencecode1)
fcovariate(Formulationcode())
fcovariate(Periodcode())
fcovariate(Sequencecode)
fixef(tvAlpha = c(, 1, ))
fixef(dAlphadFormulationcode1(enable=c(0)) = c(, 0, ))
fixef(dAlphadPeriodcode1(enable=c(1)) = c(, 0, ))
fixef(dAlphadSequencecode1(enable=c(2)) = c(, 0, ))
ranef(diag(nAlphax0) = c(1), same(nAlphax1))
}

2.8“Run Options（运行选项）”选项卡的设置

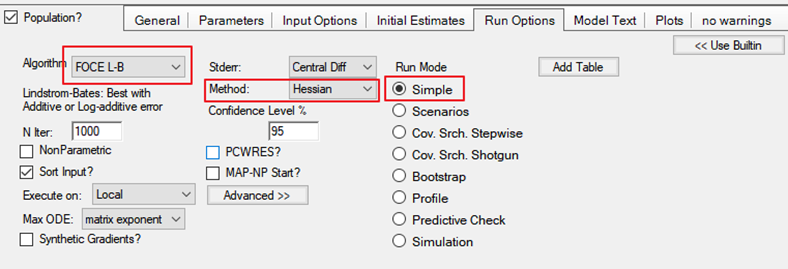
3执行模型

4模型结果

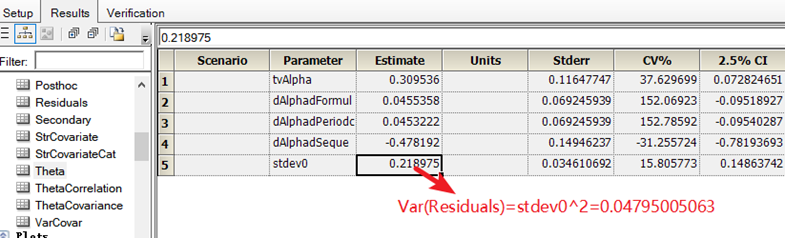
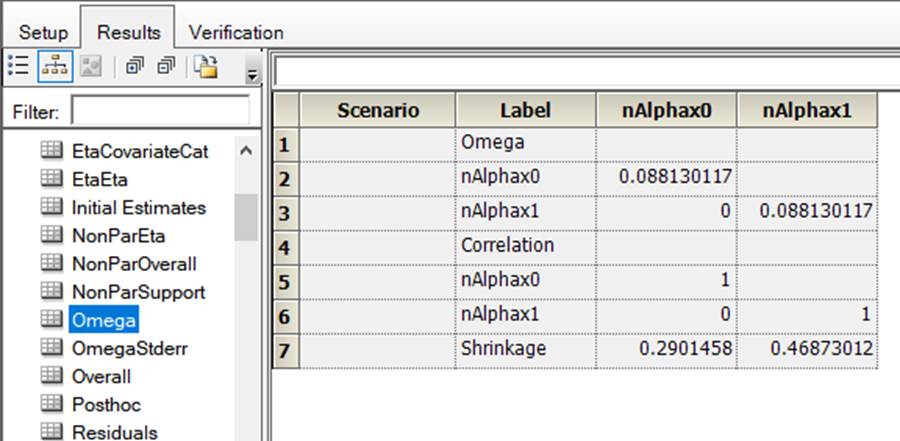
F、结果对比

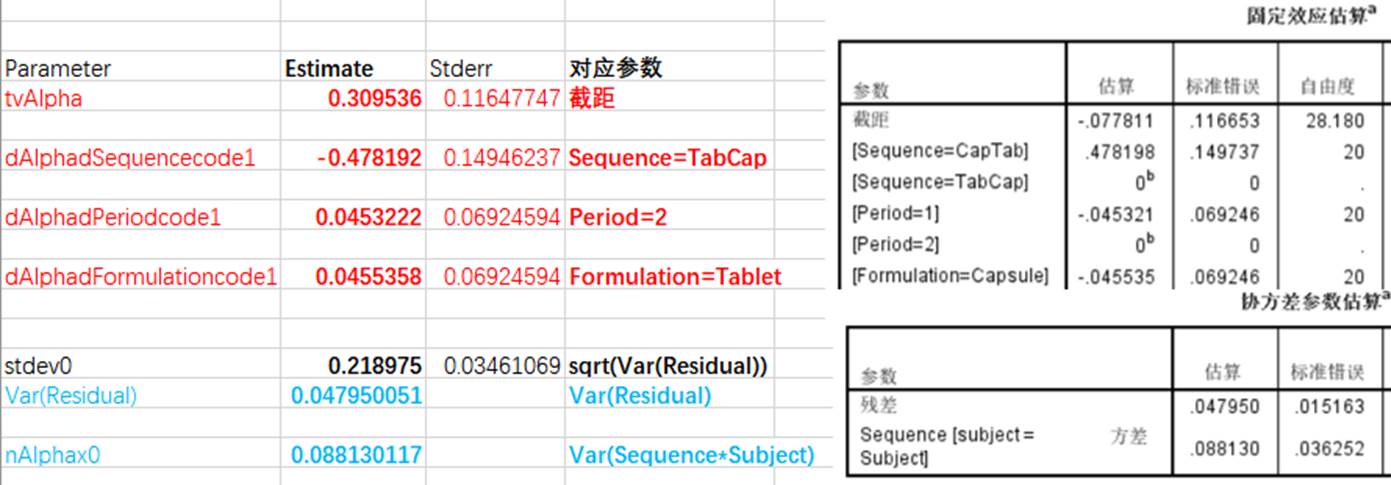
仔细核对了下，

固定效应参数，至少前5位有数数字都一样；

随机效应方差，至少前5位有数数字都一样；

得到的这样的结果我觉得已经很满意了，必定"线性混合效应模型"和"非线性混合效应模型"实现的软件、算法细节可能都不太一样，所以个人认为这可以算使用"非线性混合效应模型"重现出BE数据分析的结果了。

G、以上就是使用Phoenix Model实现对2*2试验设计生物等效性数据分析的过程，大家可以帮忙看下，上述过程可有疏漏之处~

对于2*4试验设计实现的过程暂时不发布，为其中很多步骤的处理不知道是否应该，导出的结果有硬凑的嫌疑。