前言：

在上篇案例中，我们通过“线性混合效应（Linear Mixed Effect）”操作对象构建除了一个随机截距模型，来说明他与PopPK的一些联系，我们知道提到混合效应模型，总是绕不开“收缩”这一概念，那此模型的收缩值该如何计算呢？

正文：

我不打算自己推导，直接拿来主义。

收缩值的其他计算公式：

参考文献指出，随机截距的模型的收缩可以这样计算：

方差形式：

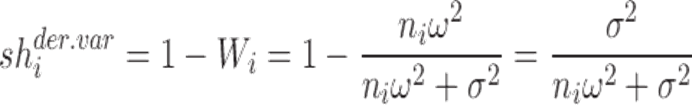
标准差形式：

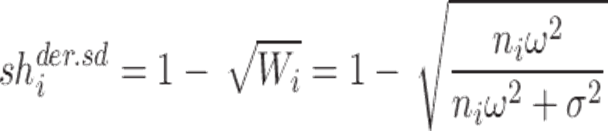
引自：Shrinkage in Nonlinear Mixed-Effects Population Models: Quantification, Influencing Factors, and Impact

所以，通过公式可以很明显的看出，收缩值的大小与ω和σ的相对大小有关，ω比σ越大，收缩值越小，反之越大；他们相等的时候，收缩值是多少呢？

容易计算出来，

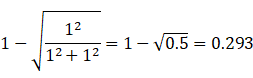
非常接近0.3，我想这就是所谓的经验性的要求收缩至小于0.3的要求的来源~！

通过类似的计算，可知，上篇文献中线性混合效应模型的收缩值为：21.4%

讨论：

我们来看看ω和σ在不同相对大小下标准差版收缩至的情况：

• 假定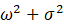=1，

• 然后指定不同的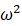值，并计算所对应的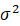值，

• 然后计算方差的比值与收缩值。

可以看到：

当标准差版收缩≈30%，“个体间变异”的方差 约等于 “个体内变异”的方差。

当标准差版收缩≈45%，“个体间变异”的方差 约是 “个体内变异”的方差的 一半。

当标准差版收缩≈16%，“个体间变异”的方差 约是 “个体内变异”的方差的 一倍。

当标准差版收缩≈68%，“个体间变异”的方差 约是 “个体内变异”的方差的 九分之一。

当标准差版收缩≈ 5%，“个体间变异”的方差 约是 “个体内变异”的方差的 九倍。

所以通篇说了这么多，有啥直观意义呢？

直观的意义就是，

1. 我们所收集数据质量的好坏，会直接影响我们可以识别出来的最小的个体间变异，

2. 如果没有我们收集到的质量很烂，由于记录时间的偏差、分析方法的变差、服药时间记录的偏差等导致的个体内变异很高，这会导致我们很难识别出一些参数的个体间变异，导致我们模型建立过程很痛苦。

3. 一般认为，参数的个体间变异是大于个体内变异的。

4. 所以通常提到“收缩值>30%表明个体层面的信息不足”，翻译为大白话就是，你的数据分析得到的个体内变异太大了，识别不了比个体内变异更小的个体间变异的参数；所以，要么重新做实验获取更高质量的数据，要么放弃对这个个体间变异参数的估计。