CAR T的细胞动力学模型

付永超 / 2021-12-15

CAR-T的细胞动力学模型

引言

CAR-T细胞是最近的一个研发热点，但对该类产品所对应的细胞动力学模型并不多，但也有相关发表报道的模型，今天选取其中一篇，将其中提到的模型在Phoenix软件中通过“ML Model操作对象(Phoenix Model操作对象)”使用的“PML”语言实现一遍，以供各位同仁方便使用。

文献来源

Model-Based Cellular Kinetic Analysis of Chimeric Antigen Receptor-T Cells in Humans（基于模型的人嵌合抗原受体-T细胞的细胞动力学分析）

https://ascpt.onlinelibrary.wiley.com/doi/abs/10.1002/cpt.2040

模型背景

CAR-T疗法，描述CAR-T的难点，与传统PK模型的区别

CAR-T疗法：

“嵌合抗原受体(CAR)-T细胞”治疗包括过继转移转基因的自体T细胞，以通过内源性细胞毒性效应细胞机制促进抗原特异性细胞杀伤。与经典药代动力学(PK)可以描述的规范药物治疗不同，CAR-T细胞经历超过输注细胞剂量的几个对数的快速扩增，并表现出不遵循典型新陈代谢和清除模型的长期持久性。

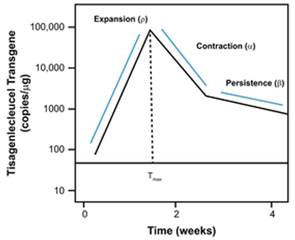
图表, 折线图描述已自动生成

描述CAR-T的难点：

经典的药理药剂，如小分子或单克隆抗体，可以用标准的隔室方法来描述以估计PK参数。小分子和单克隆抗体的分布、代谢和排泄在很大程度上是由分子的生物物理性质和吸收后产生的血浆浓度驱动的。然而，基于细胞的治疗的动力学更加复杂，并且受到靶细胞类型的生理功能和细胞外部因素的影响，例如体内CAR靶分子的丰度。

与传统PK模型的区别

与传统药物不同，CAR-T细胞具有增殖能力。因此，传统的PK参数(清除率和分布容积积)不适用，也没有作为NCA的一部分进行计算。

对于一种典型的药物，α和β斜率是由两个过程相互作用产生的，即药物从血液分布到周围组织和药物从体内排出。然而，T细胞从体内清除是由根本不同的机制控制的。α斜率对应于快速收缩，因为大多数激活的淋巴细胞在初始免疫反应后程序性凋亡，而β斜率对应于记忆细胞的逐渐下降，这些记忆细胞可以在体内持续数年甚至数十年。尽管”tisagenlecleucel(一种药品的名称)”的持续期具有与长期记忆细胞相似的动力学，但持续也可能是持续产生表达CD19B细胞前体的结果，替代抗原充当内源性疫苗。在这方面，CD19 CAR-T细胞的长期存续期可能类似于针对潜伏病毒(如巨细胞病毒)的T细胞。

属性	小分子	CAR-T细胞 17，24
增殖能力	否	是
α和β阶段的原因	分布和消除	收缩与持久化
终末半衰期时间尺度	小时、天或周	年
传统NCA参数(清除率和分布容积积)的适用性	适用	不适用，因为CAR-T细胞具有增殖能力
产品在不同患者间的变异	无	变异的存在是由于患者免疫系统的变异性
明确剂量和暴露之间的关系	是的，尽管它可能是非线性的	检测到的剂量和暴露之间没有关系
口服小分子或静脉注射CAR-T细胞剂量后的动力学方程	AEXP(-αt)+BEXP(-βt)-(A+B) EXP(-Kat)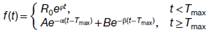
给药后初始增加的指数符号	负(-ka)	正(+ρ)

文献所提及的模型

模型1：基础模型（一种描述所观察到的曲线特征的经验模型）
模型2：一种半机制的模型（能过够解释曲线特征的一种半机制模型，有多种学术都能够解释这种曲线特征，此处仅是举例）
模型3：重新参数化的基础模型（文献并无直接展示，但其实隐含了这一模型，该模型在基础模型之上通过半机制模型对原有参数进行了重新参数化）
模型4：最终模型（在重新参数化的基础模型之上引入协变量）

几个模型之间的演化关系

总体演化过程

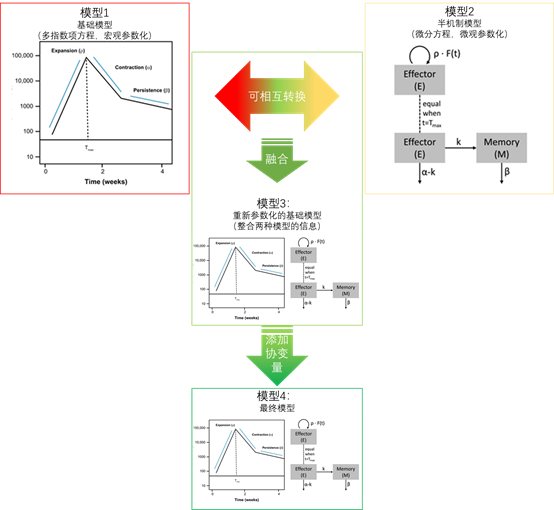
图片包含图形用户界面描述已自动生成

模型1：基础模型

文本中度可信度描述已自动生成

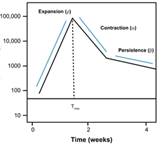
模型2A：一种半机制模型

图形用户界面, 应用程序, Teams 描述已自动生成

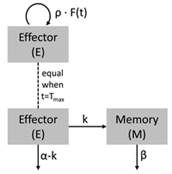
模型3：重新参数化的基础模型

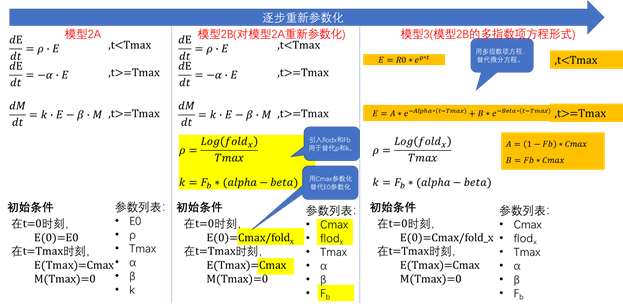
文本, 日程表描述已自动生成

模型3介绍

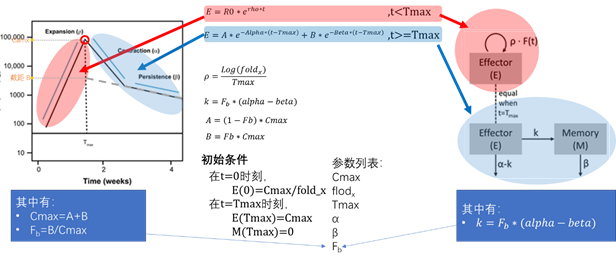
图形用户界面低可信度描述已自动生成

模型4：最终模型（模型3+协变量）

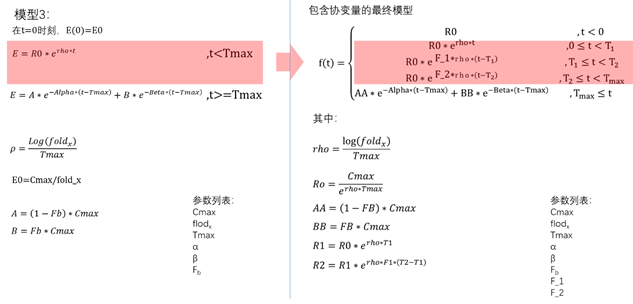
箭头中度可信度描述已自动生成

在Phoenix中的实现

模型1

模型的方程：

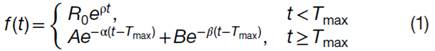
对应的典型曲线：

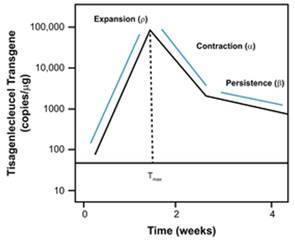
图表, 折线图描述已自动生成

PML代码

test(){
     covariate(tt)

     E=(
          (tt<Tmax)?
              Ro*exp(p*tt)
          :
              A*exp(-Alpha*(tt-Tmax))+B*exp(-Beta*(tt-Tmax))
     )

     error(EEps = 2.66295001310029)
     observe(EObs(tt) = E + EEps)
 
stparm(Tmax=tvTmax)
stparm(Ro=tvRo)
stparm(p=tvp)
stparm(A=tvA)
stparm(Alpha=tvAlpha)
stparm(B=tvB)
stparm(Beta=tvBeta)

fixef(tvTmax=c(,19.8649961319143,))
fixef(tvRo=c(,6.43092405192262,))
fixef(tvp=c(,0.0421269627420855,))
fixef(tvA=c(,1.73947096587749,))
fixef(tvAlpha=c(,0.109143920526125,))
fixef(tvB=c(,9.05116731581526,))
fixef(tvBeta=c(,0.002539845458873,))
}

其中：

F(t)，随时间变化的细胞在体内的数量
R0，0时刻体内可用于扩张/增值的细胞的数量
p，从0时刻至Tmax时刻，细胞在体内的扩张的1级速率常数

Tmax后曲线呈双指数函数特征，即类似于血管内给药二房室模型宏观参数化，由此易知：

A+B=Cmax

曲线末端对数尺度下的斜率约等于（-Beta）

所以，

A，快速下降过程的截距
B，慢速下降过程的截距
Alpha，快速下降过程的速率
Beta，慢速下降过程的速率
EEps，残差变异的方差

注意事项

文献未报告参数的初始值与估计值。

典型曲线图

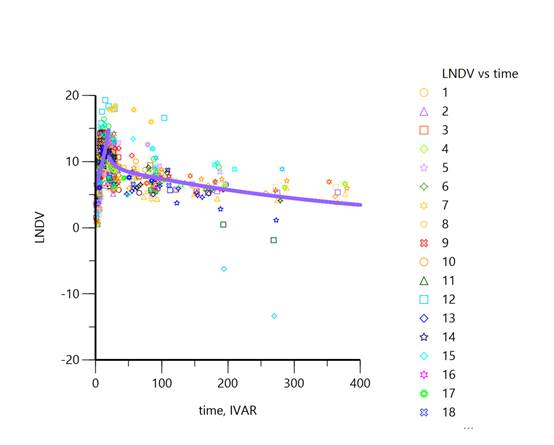
图表, 散点图描述已自动生成

讨论，

可以观察到，此模型可以很好的描述出曲线的典型趋势。

模型2B

模型方程：

模型对应的结构示意图：

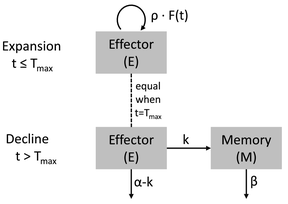
图示描述已自动生成

其中：

E+M，随时间变化的细胞在体内的总数量
E，细胞中发生效用的细胞的量
M，细胞中用于记忆的细胞的量
p，从0时刻至Tmax时刻，细胞在体内的扩张的1级速率常数
Alpha，快速下降过程的速率
Beta，慢速下降过程的速率
k，效用细胞转化为记忆细胞的一级速率常数
E0，0时刻体内可用于扩张/增值的细胞的数量（基础模型中称之为R0）
Cmax，Tmax时刻细胞在体内的总量
Fold_x，折叠系数

Fold_x、p、Cmax、Tmax间的关系：

对于曲线的上升段可有以下公式：

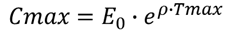
进而可推导出：

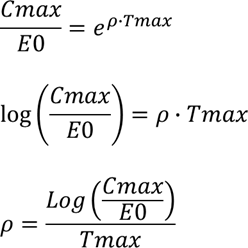
令

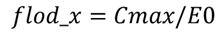
则有

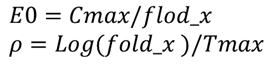
k的推导公式：

由上述联立的方程可求得

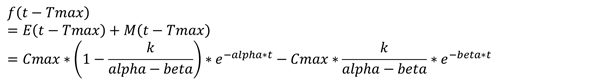
即

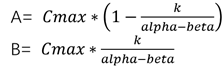
又知道

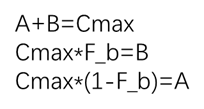
由此可得：

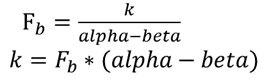
从而得到完整的方程：

PML代码

test(){
deriv(E=t<Tmax?p*1*E:-Alpha*E)
deriv(M=t<Tmax?0:k*E-Beta*M)
 
p=log(fold_x)/Tmax
k=F_b*(Alpha-Beta)

sequence{
     E=Cmax/fold_x;
sleep(Tmax);
     E=Cmax
     M=0
}

error(EEps = 1)
observe(EObs = E + EEps)

stparm(Tmax=tvTmax*exp(nTmax))
stparm(Cmax=tvCmax*exp(nCmax))
stparm(fold_x=tvfold_x*exp(nfold_x))
stparm(Alpha=tvAlpha*exp(nAlpha))
stparm(Beta=tvBeta*exp(nBeta))
stparm(F_b=tvF_b*exp(nF_b))

fixef(tvTmax=c(,9.3,))
fixef(tvCmax=c(,24000,))
fixef(tvfold_x=c(,3900,))
fixef(tvAlpha=c(,0.16,))
fixef(tvBeta=c(,0.0032,))
fixef(tvF_b=c(,0.0079,))

ranef(diag(nTmax,nCmax,nfold_x,nAlpha,nBeta,nF_b)=c(1,1,1,1,1,1))
}

注意事项

文献未报告参数估计值

模型3

模型3是在模型1的基础上，利用模型2对原有的参数进行重新参数化后得到的。

模型的方程

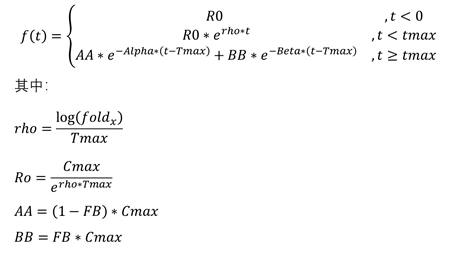
PML代码

test(){
     covariate(tt)
     
     rho=log(fold_x)/Tmax

     Ro=Cmax/exp(rho*Tmax)
     AA=(1-FB)*Cmax

     BB=FB*Cmax

     E=
     tt<0?
          Ro:
     tt<Tmax?
          Ro*exp(rho*tt):
     AA*exp(-Alpha*(tt-Tmax))+BB*exp(-Beta*(tt-Tmax))

     logE=log(E)

     error(EEps = 0.56)
     observe(EObs(tt)=logE*(1+EEps))

     stparm(Tmax=tvTmax*exp(nTmax))
     stparm(Cmax=tvCmax*exp(nCmax))
     stparm(fold_x=tvfold_x*exp(nfold_x))
     stparm(Alpha=tvAlpha*exp(nAlpha))
     stparm(Beta=tvBeta*exp(nBeta))
     stparm(FB=tvFB*exp(nFB))

     fixef(tvTmax=c(,9.3,))
     fixef(tvCmax=c(,24000,))
     fixef(tvfold_x=c(,3900,))
     fixef(tvAlpha=c(,0.16,))
     fixef(tvBeta=c(,0.0032,))
     fixef(tvFB=c(,0.0079,))

     ranef(diag(nTmax,nCmax,nfold_x,nAlpha,nBeta,nFB)=c(0.38,0.65,2.4,0.91,0.86,0.8))
}

模型4：包含协变量的最终模型

模型的方程

PML代码

test(){

covariate(tt)
fcovariate(TOCI1T)
fcovariate(STERSTT)

t1_TOC_OR_Tmax=min(TOCI1T,Tmax)
t1_STE_OR_Tmax=min(STERSTT,Tmax)
t2_TOC_OR_Tmax=min(TOCI1T,Tmax)
t2_STE_OR_Tmax=min(STERSTT,Tmax)
t1=TOCI1T<=STERSTT?t1_TOC_OR_Tmax:t1_STE_OR_Tmax
t2=TOCI1T<=STERSTT?t2_STE_OR_Tmax:t2_TOC_OR_Tmax

F1=TOCI1T<=STERSTT?Ftoci:Fster
F2=TOCI1T<=STERSTT?Fster:Ftoci

rho=log(fold_x)/Tmax
R0=Cmax/exp(rho*Tmax)
R1=R0*exp(rho*t1)
R2=R1*exp(F1*rho*(t2-t1))
CmaxAdjust=R2*exp(F1*F2*rho*Tmax-t2)

AA=(1-FB)*CmaxAdjust
BB=FB*CmaxAdjust

E=tt<0?R0:tt<t1?R0*exp(rho*tt):tt<t2?R1*exp(F1*rho*(tt-t1)):tt<Tmax?R2*exp(F1*F2*rho*(tt-t2)):AA*exp(-alpha*(tt-Tmax)) + BB*exp(-beta*(tt-Tmax))

    \#observe(Eobs(tt)=log(E)+CEps)

observe(Eobs(tt)=E*exp(CEps))

error(CEps = 0.56)

stparm(Tmax=tvTmax*exp(nTmax))
stparm(Cmax=tvCmax*exp(nCmax))
stparm(fold_x=tvfold_x*exp(nfold_x))
stparm(alpha=tvAlpha*exp(nAlpha))
stparm(beta=tvBeta*exp(nBeta))
stparm(FB=tvF_b*exp(nF_b))
stparm(Ftoci=tvFtoci)
stparm(Fster=tvFster)

fixef(tvTmax=c(,9.3,))
fixef(tvCmax=c(,24000,))
fixef(tvfold_x=c(,3900,))
fixef(tvAlpha=c(,0.16,))
fixef(tvBeta=c(,0.0032,))
fixef(tvF_b=c(,0.0079,))
fixef(tvFtoci=c(,1.2,))
fixef(tvFster=c(,1,))

ranef(diag(nTmax,nCmax,nfold_x,nAlpha,nBeta,nF_b)=c(0.38,0.65,2.4,0.91,0.86,0.8))
}

注意事项

对文献报告参数之中个体间变异的假定

VPC图

对文献所附带的一组示例数据集绘制VPC的结果

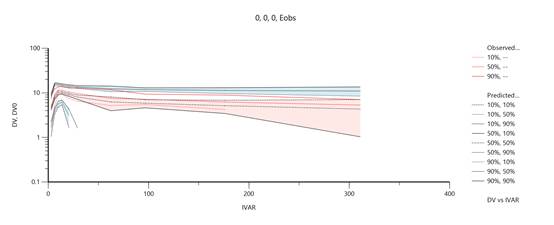
图片包含图表描述已自动生成

文献所报道的参数值：

类别	参数	单位	估计值	百分化的相对标准误	个体间变异收缩值
固定效应参数	foldx	—	3,900	30	—
固定效应参数	T max	Days	9.3	4.2	—
固定效应参数	C max	DNA copies/μg	24,000	20	—
固定效应参数	F toci	—	1.2	7.5	—
固定效应参数	F ster	—	1	9	—
固定效应参数	α	1/day	0.16	11	—
固定效应参数	F B	—	0.0079	15	—
固定效应参数	β	1/day	0.0032	23	—
随机效应参数	foldx	—	2.4	9.5	0.39
随机效应参数	T max	—	0.38	7.9	0.14
随机效应参数	C max	—	0.65	10	0.29
随机效应参数	α	—	0.91	8.8	0.27
随机效应参数	F B	—	0.8	15	0.53
随机效应参数	β	—	0.86	23	0.82
残差	a	—	0.56	3.3	—

讨论：

模型1：基础模型

优点：非常清晰的模型解析表达式，可以很好的描述曲线特征
缺点：模型的参数是一些纯粹的数学参数，没有直观的生理意义，模型参数较多。
参数数量：7
参数：R0，ρ，Tmax， α，β，A，B，

模型2：一种半机制模型

优点：采用了一种假说，可以通过直观的结构示意图展示出模型，以及参数的含义，并且参数更少
缺点：是微分方程形式，不是解析表达式
参数数量：6
参数：E0，ρ，Tmax， α，β，k

模型3：重新参数化的基础模型

优点：通过“模型2”重新对“模型1”参数化，使获得参数有生理意义，并且具有解析表达式
缺点：
参数数量：6
参数：Cmax，flod_x，Tmax， α，β，FB

我对这个案例的耐心耗尽了，不想再投入更多的时间去组织素材、优化语言表达了，此案例看起来可能很痛苦，就这样吧。

小结：

其实可以发现，整篇文章绕来绕去，其实都是在使用的最初的经验模型，后面一些列的操作都是在为最初的经验模型赋予更多的主观认为的一些意义，这是由于，1该经验模型确实优秀良好，2CAR-T的机制及其对机制模型的抽象总结还不完善所致的。

所以可以预见的短期未来，在良好简介的机制模型出现之前，对其细胞动力学的分析仍然后主要以最开始的经验模型为主，当然，不同的作者可能对该经验模型所对应的机制假说有不同的解读，从而产生一些如同本文一样的衍生的模型。

CAR-T的细胞动力学模型

引言

目录

文献来源

模型背景

CAR-T疗法：

描述CAR-T的难点：

与传统PK模型的区别

文献所提及的模型

几个模型之间的演化关系

总体演化过程

模型1：基础模型

模型2A：一种半机制模型

模型3：重新参数化的基础模型

模型4：最终模型（模型3+协变量）

在Phoenix中的实现

模型1

模型的方程：

对应的典型曲线：

PML代码

其中：

注意事项

典型曲线图

讨论，

模型2B

模型方程：

模型对应的结构示意图：

其中：

Fold_x、p、Cmax、Tmax间的关系：

k的推导公式：

从而得到完整的方程：

PML代码

注意事项

模型3

模型的方程

PML代码

模型4：包含协变量的最终模型

模型的方程

PML代码

注意事项

VPC图

文献所报道的参数值：

讨论：

小结：