文献_定量药理学中的协变量建模_附件1和附件2
付永超 / 2024-06-24
原文链接：https://ascpt.onlinelibrary.wiley.com/doi/10.1002/psp4.13115
原文作者：Kinjal Sanghavi, Jakob Ribbing, James A. Rogers, Mariam A. Ahmed, Mats O. Karlsson, Nick Holford, Estelle Chasseloup, Malidi Ahamadi, Kenneth G. Kowalski, Susan Cole, Essam Kerwash, Janet R. Wade, Chao Liu, Yaning Wang, Mirjam N. Trame, Hao Zhu, Justin J. Wilkins, for the ISoP Standards & Best Practices Committee
原文协议：CC BY-NC 4.0
译者注：主要由Edge浏览器自带的网页翻译功能翻译，译者额外校对了部分词汇的中文翻译比如“pharmacodynamics”在本文应翻译为“药效动力学”，而不是“药效学”。
目录
附件一：
图示ISOP的最佳实践：定量药理学中的协变量分析——使用茶碱数据案例研究
1 引言
本文档在一定程度上说明了本文中介绍的不同协变量选择方法。使用真实的纵向药效动力学数据：在给予药物茶碱的临床试验期间收集的“呼气峰值流速（PEFR, peak expiratory flow rate）”测量值。该文档分为介绍数据（第2节）、模型（第3节）、不同协变量选择方法的结果（第4节）、诊断协变量效应的一些示例（第5节）以及如何呈现协变量模型的示例（第6节）。模型部分仅详细介绍了已发布的带有协变量的模型，该模型用作这项工作的起点[1]，没有协变量的衍生基础模型用作大多数协变量选择方法的起点，以及完整的固定效应模型（FFEM）。但是，所有代码都在文档的附录中报告：附录A中的NONMEM模型代码，附录B中的R代码。
协变量模型的默认参数化方式会因所选方法中的可用实现而不同。
2 茶碱数据
2.1 数据说明
茶碱数据由NickHolford提供[1,2]。细节和实验设计详见其他地方报道[2]，摘要如下。用于准备分析数据的R代码可在附录B.1中找到。从数据集中删除了缺失信息的行，缺失信息的范围在初始出版物中提供[1]。本说明练习仅保留了四个协变量（两个分类和两个连续）。
符合静脉注射茶碱治疗条件的急性气道阻塞患者被随机分配到目标浓度为10或20mg/L的双盲试验中。初始剂量和随后的调整由每位患者的医生使用实际茶碱浓度的缩放报告确定，以保持盲法但模仿实际临床实践。在最初的24小时内多次获得“呼气峰值流速（PEFR, peak expiratory flow rate）”和茶碱浓度，并且至少每天获得一次，直到出院。
表S1提供了数值描述。每个受试者的平均采样次数为4次。用于计算数值汇总的R代码在附录B.2中提供，有关数据文件的更多详细信息见附录B.3：表S9中对数据文件的描述，以及表S10中前十行的概述。
表格 S1：茶碱数据集的数值描述
| 变量 | 类别 | 度量* |
|---|---|---|
| 因变量(526个观测值) | ||
| 茶碱浓度(mg/L) | 13 (8, 18) | |
| 呼气峰值流速(PEFR, L/min) | 220 (160, 300) | |
| 连续协变量(132个受试者) | ||
| 年龄(years) | 34.5 (21.0, 55.0) | |
| 体重(kg) | 66.0 (56.0, 76.0) | |
| 分类协变量(132个受试者) | ||
| 性别 | 0:女性 | 82.0 (62.1%) |
| 1:男性 | 50.0 (37.9%) | |
| 诊断 | 1:哮喘 | 108.0 (81.8%) |
| 2:慢性阻塞性肺病 | 22.0 (16.7%) | |
| 3: COPD和哮喘 | 2.0 (1.5%) |
* 连续变量的中位数（四分位距）;n（%） 表示分类变量。
2.2 图形探索
2.2.1 因变量：意大利面条图
观察到的药效动力学数据（即PEFR）与时间的关系图如图S1所示，与浓度的关系图如图S2所示。用于图S2的R代码可在附录B.4中找到。
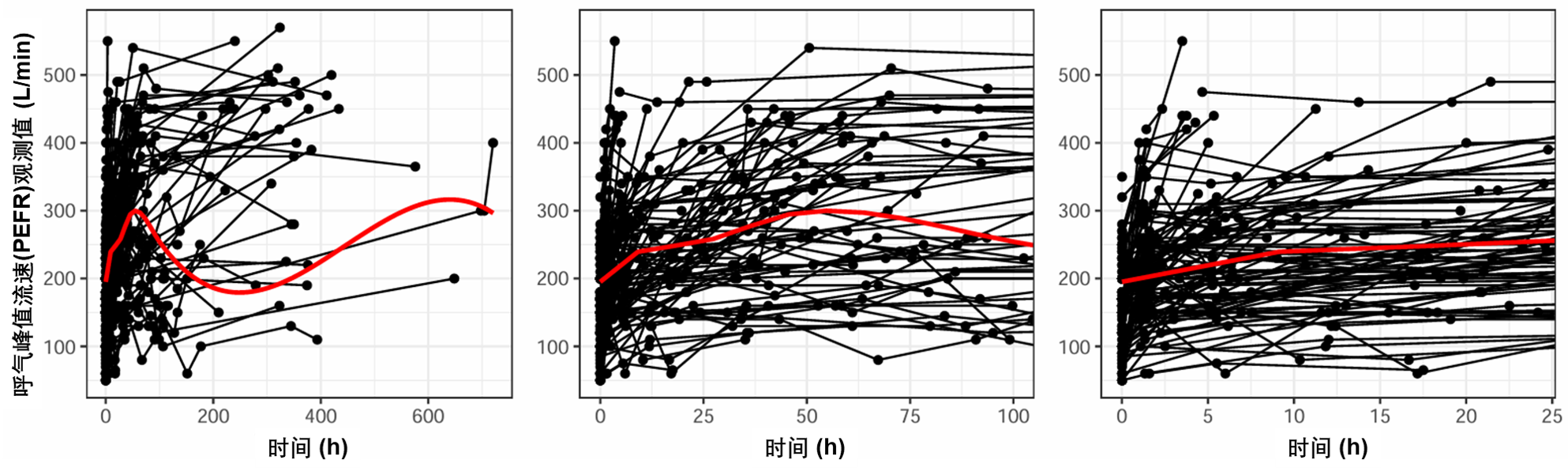图S1：观察到的“呼气峰值流速（PEFR, peak expiratory flow rate）”与时间的关系。点代表观测值，每个人的观测值都由一条线连接。红线是平滑的。数据使用正常比例显示，在前100小时（中面板）上缩放，在前25小时（右面板）上缩放。PEFR：峰值呼气流速。
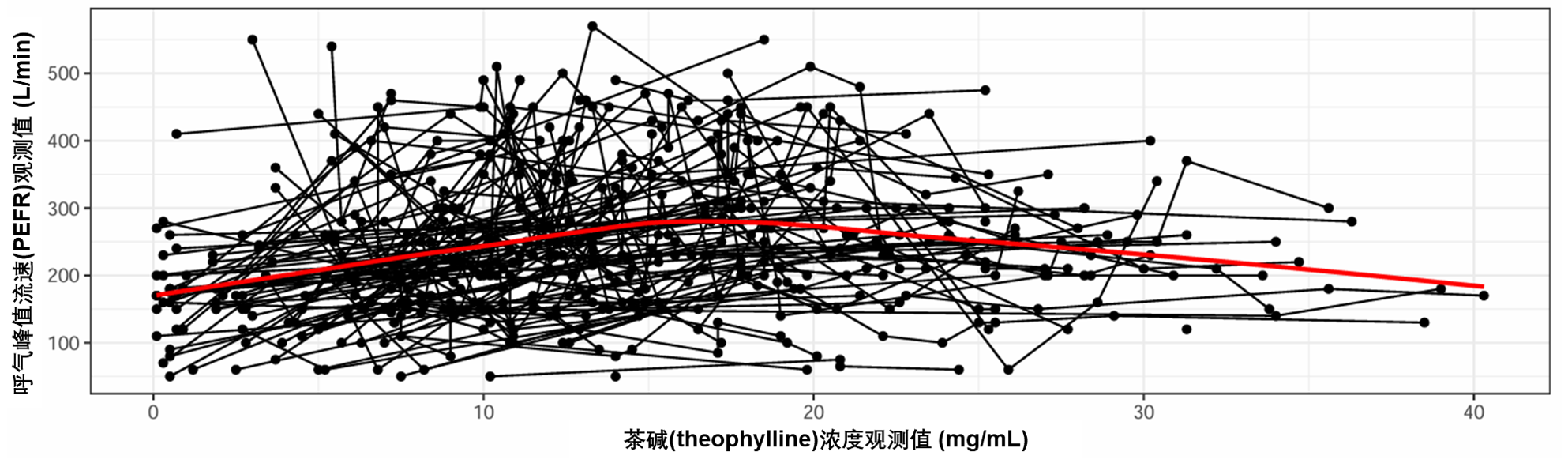图S2：观察到的“呼气峰值流速（PEFR, peak expiratory flow rate）”与观察到的茶碱血清浓度。点代表观测值，每个人的观测值都由一条线连接。红线是平滑的。数据使用正常比例显示。PEFR：峰值呼气流速。
2.2.2 协变量：散点图矩阵
散点图矩阵（图S3）显示了每对协变量之间的关系。用于生成散点图矩阵的R代码在附录B.5中提供。
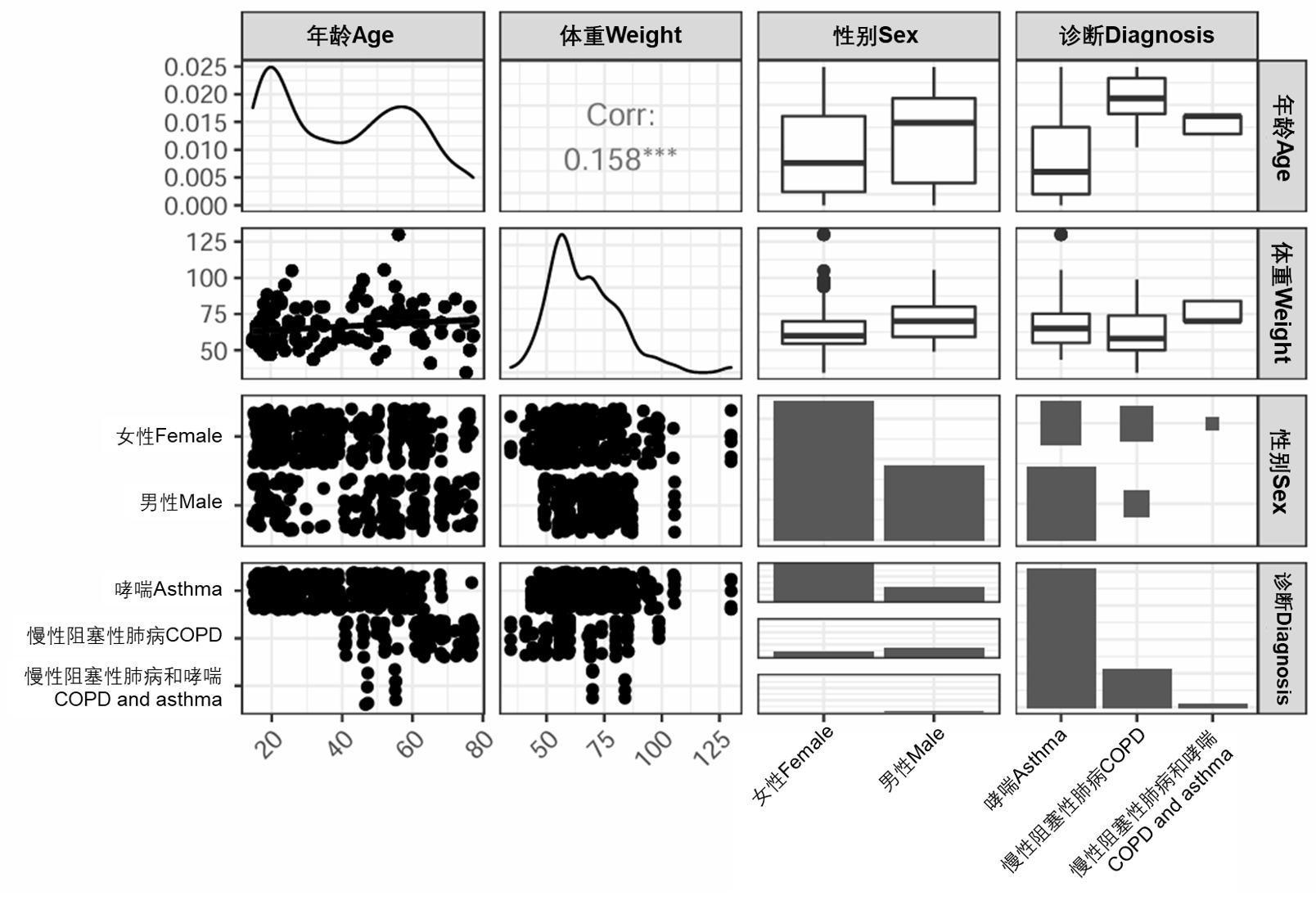图S3：对每对可用协变量之间关系的可视化探索。对角线图表示每个协变量的分布。
3模型
“呼气峰值流速（PEFR, peak expiratory flow rate）”的药效动力学模型是根据先前的出版物[1]开发的，没有（run11）或协变量（run20）。从无协变量的模型出发，根据不同的协变量选择方法构建了不同的协变量模型，以提供说明性算例。获得的不同模型以及最终参数数列在表S4中。
3.1出版物中的模型
先前在已发表的论文中的参数模型被复制为表S4中的run20。参数值如表S2所示，NONMEM代码见附录A.1。此处显示的run20与已发布的模型不同，因为通过删除缺少数据的行来减小数据集。
如已发表的论文所述，支气管狭窄因子（BCF，broncho-constriction factor）通过一阶过程消除，其特征是半衰期T50和基线BCF0值（方程（1））。根据方程（2）中描述的抑制性药效动力学模型，PEFR（t）是由于BCF引起的支气管收缩，与BCF浓度有关，其中Normal是BCF为零时的PEFR，C50BCF是使PEFR从正常降低50%的浓度。假设Base是t=0时的PEFR，方程（3）给出了此时BCF的浓度（BCF0）。茶碱对PEFR的影响仅限于低于正常的PEFR，并根据方程（4）表示，其中C50_Theo是茶碱浓度C产生50%的潜在可回收PEFR时的值，Hill是控制曲线陡峭度的指数。BCF和茶碱对PEFR的综合影响可以通过时间和茶碱浓度的函数来预测，如式（5），其中ε_theo描述了茶碱相对于BCF介导的时间效应的疗效。
所有协变量均线性添加到Normal典型值。分类诊断协变量作为连续协变量包含在已发布的模型中，使用分配给每个类别的数值。在本文档中提供的示例中，只要有可能，它就被作为分类协变量包含在内。
$$ BCF (t) = BCF0 \cdot e^{(-ln(2)/(T50 \cdot))} \tag{1} $$ $$ PEFR(t) = Normal \cdot [ 1- \frac{BCF(t)}{BCF(t)+C50_{BCF}} ] \tag{2} $$ $$ BCF_0=C50_{BCF} \cdot ( Normal/Base -1 ) \tag{3} $$ $$ PEFR(c,t) = [Normal – PEFR(t)] \cdot \frac{C^{Hill}}{ C^{Hill} + C^{Hill}_{Theo} } \tag{4} $$ $$ PEFR = PEFR(t) + ε_{theo} \cdot PEFR(c,t) \tag{5} $$表格 S2: 出版物中的协变量模型参数表（run20）.
| 参数 | 描述 | 单位 | 数值 | 相对标准误* | 收缩值 (%) |
|---|---|---|---|---|---|
| Base | 基线时的呼气峰值流速(PEFR) | L/min | 136 | 0.0642 | - |
| Normal | 在不包含支气管狭窄因子(BCF)下的呼气峰值流速(PEFR)† | L/min | 481 | 0.0621 | - |
| T50 | 支气管狭窄因子(BCF)的半衰期 | h | 19.6 | 0.263 | - |
| C50 | 生产50%的可回收呼气峰值流速(PEFR)时的茶碱浓度 | mg/L | 8.48 | 0.268 | - |
| ε**theo | 茶碱相对于支气管狭窄因子(BCF)效应的疗效 | - | 0.373 | 0.197 | - |
| Hill exponent | 曲线陡度指数 | - | 2.59 | 0.3 | - |
| Diagnosis on Normal | 每个类别的典型值分数 | - | 0.202 | 0.174 | - |
| Female on Normal | 女性的典型值分数 | - | -0.258 | 0.193 | - |
| Years on Normal | 缩放因子 | - | -0.012 | 0.12 | - |
| IIV Base | - | 0.405 | 0.256 | 18.9 | |
| IIV Normal | - | 0.164 | 0.364 | 43.4 | |
| IIV T50 | - | 1.55 | 0.281 | 29.6 | |
| IIV C50 | - | 0.664 | 0.609 | 48.2 | |
| Proportional RUV | - | 0.159 | 0.123 | 25.8 |
IIV和RUV值报告为对角线元素的标准偏差。 IIV和RUV的RSE，以近似标准差标度报告（标准误差/方差估计值）/2。收缩值对应于标准差收缩。 PEFR：呼气峰值流速，BCF：支气管狭窄因子，RUV：残余的不明变异性，IIV：个体间变异，RSE：相对标准误差。SIR:抽样密集重采样。 *使用SIR获得的RSE † 典型个体:男性，40公斤，患有哮喘。
3.2 不带协变量的基础模型
从已发表的模型（run20）中删除了协变量效应，从而产生了一个没有协变量的基础模型，该模型将用作大多数协变量选择方法的起点（表S4中的run11）。参数值如表S3所示，图S4中提供了图形说明，附录A.2中提供了NONMEM代码。RSE值来自方差协方差矩阵。
表格 S3: 无协变量的 PEFR 药效动力学模型的 arameters 表 （run11）。
| 参数 | 描述 | 单位 | 数值 | 相对标准误* | 收缩值 (%) |
|---|---|---|---|---|---|
| Base | 基线时的呼气峰值流速(PEFR) | L/min | 143 | 0.0534 | - |
| Normal | 在不包含支气管狭窄因子(BCF)下的呼气峰值流速(PEFR) | L/min | 332 | 0.0546 | - |
| T50 | 支气管狭窄因子(BCF)的半衰期 | h | 9.54 | 0.37 | - |
| C50 | 生产50%的可回收呼气峰值流速(PEFR)时的茶碱浓度 | mg/L | 10.3 | 0.215 | - |
| ε**theo | 茶碱相对于支气管狭窄因子(BCF)效应的疗效 | - | 0.414 | 0.207 | - |
| Hill exponent | 曲线陡度指数 | - | 3.25 | 0.25 | - |
| IIV Base | - | 0.404 | 0.229 | 20.3 | |
| IIV Normal | - | 0.389 | 0.221 | 16.6 | |
| IIV T50 | - | 1.22 | 0.413 | 34 | |
| IIV C50 | - | 0.68 | 0.638 | 48.6 | |
| Proportional RUV | - | 0.145 | 0.14 | 30.4 |
IIV和RUV值报告为对角线元素的标准偏差。 IIV和RUV的RSE，以近似标准差标度报告（标准误差/方差估计值）/2。收缩值对应于标准差收缩。 PEFR：呼气峰值流速，BCF：支气管狭窄因子，RUV：残余的不明变异性，IIV：个体间变异，RSE：相对标准误差。 * 使用SIR获得的RSE
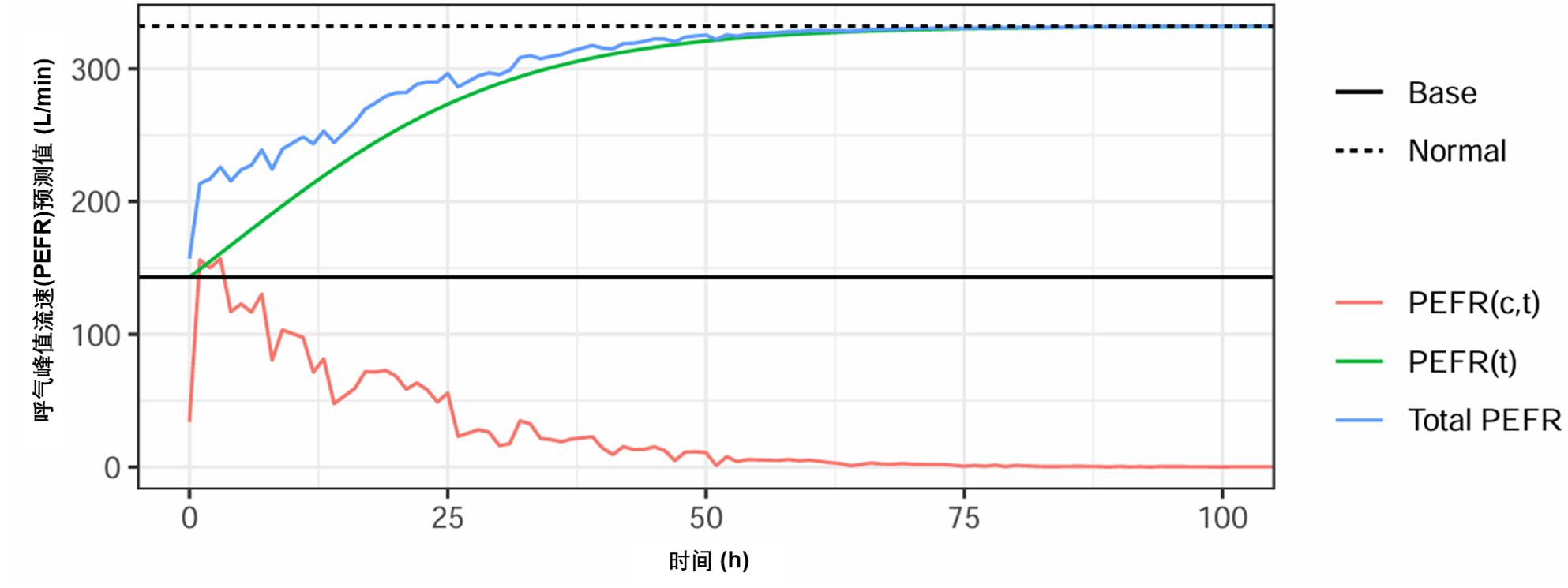图S4:使用已发表的不带协变量(run11)的模型典的型值的图形说明。Base：基线时的呼气峰值流速(PEFR)，Normal：在不包含支气管狭窄因子(BCF)下的呼气峰值流速(PEFR)，PEFR：呼气峰值流速，PEFR(t)：时间依赖性呼气峰值流速(PEFR)，PEFR(c,t)：茶碱浓度和时间依赖性呼气峰值流速(PEFR)。
表 S4：被插图说明的不同模型的详细信息。
| 描述 | 协变量范围 | 运行编号(Run nb) |
|---|---|---|
| 不带协变量的基础模型 (Base model without covariate) | 11 | |
| 出版物中的协变量模型 (Covariate model from the publication) | 20 | |
| FFEM模型 (FFEM model) | Normal和Base参数的饱和†模型 | 22 |
| 基于WAM的协变量模型 (Covariate model based on WAM) | 从FFEM模型开始 | 24 |
| 基于SCM的协变量模型 (Covariate model based on SCM) | 所有参数上的所有协变量 | 25 |
| 基于LASSO的协变量模型 (Covariate model based on LASSO) | Normal参数上的所有协变量 | 26 |
| FREM最终模型 (FREM final model) | 所有参数上的所有协变量 | 28 |
| GAM分析 (GAM analysis) | Normal参数上的所有协变量 | -* |
Run nb.: 模型标识符。 * 被确定的协变量参数关系未在新的NONMEM模型中被实现。 † 所有参数的所有协变量。
3.3 全固定效应模型(FFEM)
在两个参数（参数Base和参数Normal）上创建饱和FFEM（表S4中的run22）。参数值如表S5所示，参数-协变量关系的图形示意图见图S5，NONMEM代码见附录A.3。
Table S5: FFEM 的参数表 （run22）。
| 参数 | 描述 | 单位 | 数值 | 相对标准误* | 收缩值 (%) |
|---|---|---|---|---|---|
| Base | 基线时的呼气峰值流速(PEFR) | L/min | 165 | 0.0742 | - |
| Normal | 在不包含支气管狭窄因子(BCF)下的呼气峰值流速(PEFR)† | L/min | 421 | 0.139 | - |
| T50 | 支气管狭窄因子(BCF)的半衰期 | h | 12.3 | 0.452 | - |
| C50 | 生产50%的可回收呼气峰值流速(PEFR)时的茶碱浓度 | mg/L | 10 | 0.197 | - |
| ε**theo | 茶碱相对于支气管狭窄因子(BCF)效应的疗效 | - | 0.36 | 0.124 | - |
| Hill exponent | 曲线陡度指数 | - | 4.54 | 0.612 | - |
| Diagnosis on Base | 每个类别的典型值分数 | - | 0.0425 | 2.48 | - |
| Sex on Base | 女性的典型值分数 | - | -0.169 | 0.429 | - |
| Age on Base | 缩放因子 | - | -0.00534 | 0.394 | - |
| Weight on Base | 缩放因子 | - | 0.00598 | 0.606 | - |
| Diagnosis on Normal | 每个类别的典型值分数 | - | 0.211 | 0.294 | - |
| Sex on Normal | 女性的典型值分数 | - | -0.193 | 0.496 | - |
| Age on Normal | 缩放因子 | - | -0.0111 | 0.153 | - |
| Weight on Normal | 缩放因子 | - | 0.00643 | 0.534 | - |
| IIV Base | - | 0.375 | 0.105 | 17.4 | |
| IIV Normal | - | 0.285 | 0.139 | 25.6 | |
| IIV T50 | - | 1.03 | 0.341 | 34.5 | |
| IIV C50 | - | 0.565 | 0.158 | 52.6 | |
| Proportional RUV | - | 0.153 | 0.069 | 27.7 |
IIV和RUV值报告为对角线元素的标准偏差。 IIV和RUV的RSE，以近似标准差标度报告（标准误差/方差估计值）/2。收缩值对应于标准差收缩。 PEFR：呼气峰值流速，BCF：支气管狭窄因子，RUV：残余的不明变异性，IIV：个体间变异，RSE：相对标准误差。
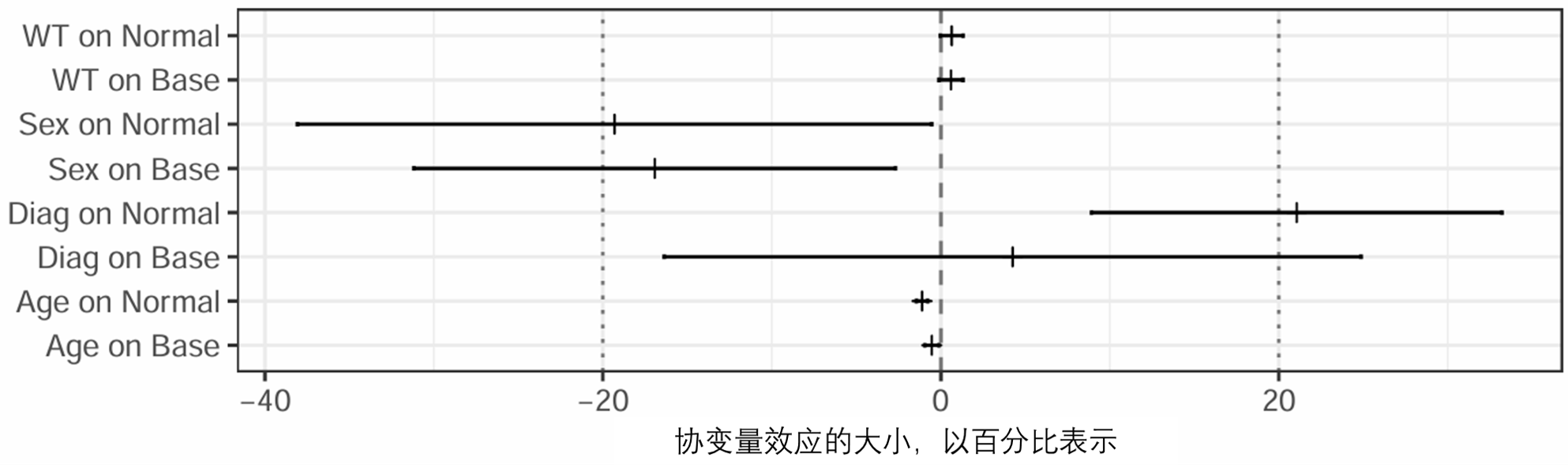图 S5: 表示协变量、固定效应估计值和不确定性的森林图，以 FFEM 的大小效应百分比表示 （run22）。
3.4 用于协变量模型的函数形式
图S6说明了连续关系的不同函数形式，相应的公式在方程 6 至 10 中表示。将不同的模型与Normal和Age数据进行拟合，从不含协变量的模型中获得个体的Normal参数值(Run 11)。
线性模型(Linear model) $y(x)=ax+b $ (6)
指数模型(Exponential model) $y(x)=ae^{bx} $ (7)
幂模型(Power model) $y(x)=ax^b $ (8)
S型模型(Sigmoid model) $y(x)=ax/(b+x) $ (9)
分片模型(Piece-wise model) $ y(x)=\left\{\begin{array}{l}a(x-\bar{x})+b &&{如果 x \leq \bar{x}} \\ c(x-\bar{x})+b &&{如果 x >\bar{x}}\end{array} \right.$ (10)
其中$\bar{x}$协变量的中位数。
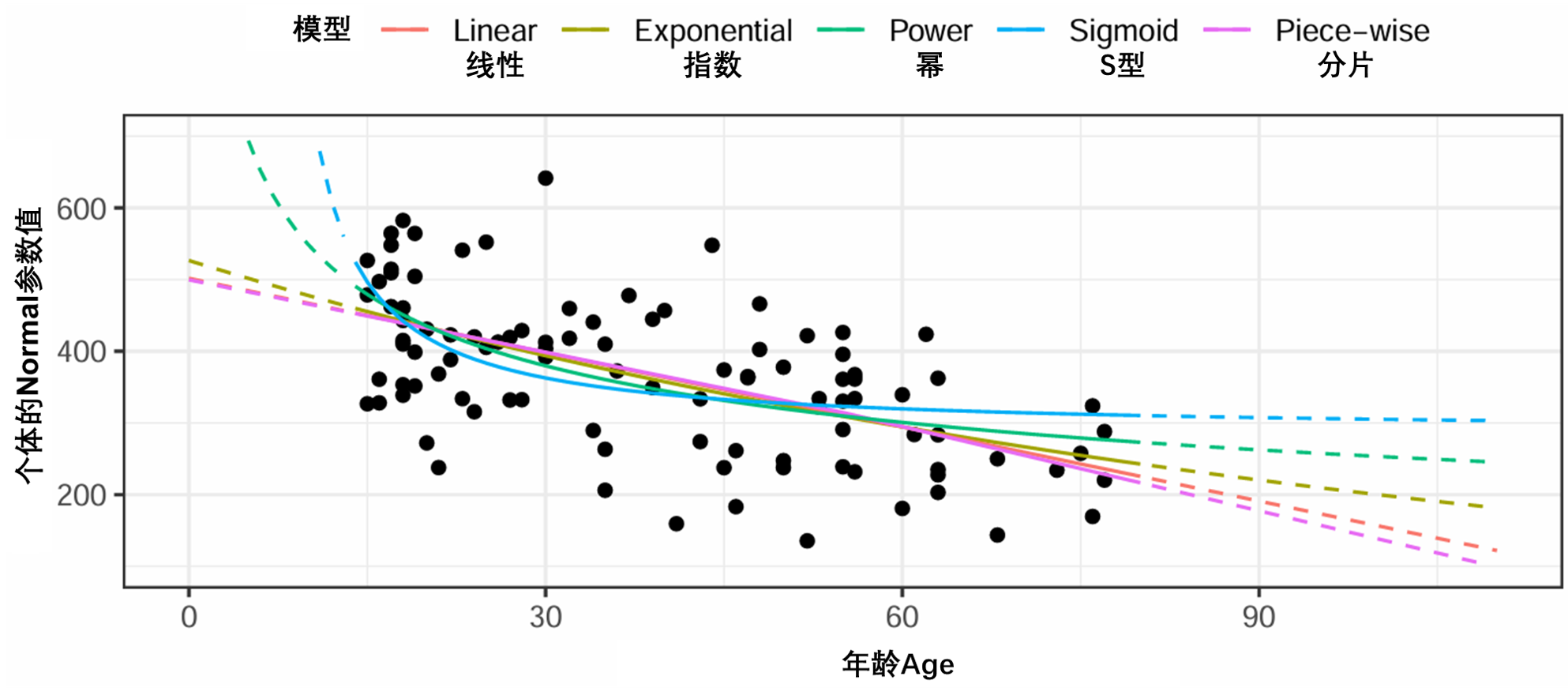图 S6:拟合Normal和Age数据的连续协变量的协变量模型示例。个体Normal值是模型中不带协变量的EBE（run11）。虚线部分表示超出观测的协变量范围的外推。EBE：经验贝叶斯估计。
4 基于模型的协变量筛选
4.1协变量与单个随机效应
可以通过包含预测变量（即协变量）来减少单个随机效应。根据可用的协变量绘制这些个体的随机效应（EBE）有助于证明参数-协变量关系，从而建议在哪个参数上包含哪个协变量。图S7的左侧面板（附录B.7中提供的R代码）显示了茶碱数据，使用第3.2节中介绍的无协变量模型（run11）。
然而，在存在重要的η收缩（根据[3]>20-30）的情况下，当用于协变量筛选时，这些图可以指示错误关系或隐藏真实关系。另一种方法是使用来自单个条件分布的随机抽样来生成η样本，而不是EBE，如[4]所示。η样本的个体均值和个体方差可在NONMEM生成的.phi文件中找到。图S7的右侧面板说明了协变量与η样本之间的关系（附录B.8中提供了R代码）。
基础模型（run11）的EBE与协变量图和η样本与协变量图的比较表明，样本的分布略有扩大。从视觉上看，线性回归的斜率没有明显的差异（见图S7）。
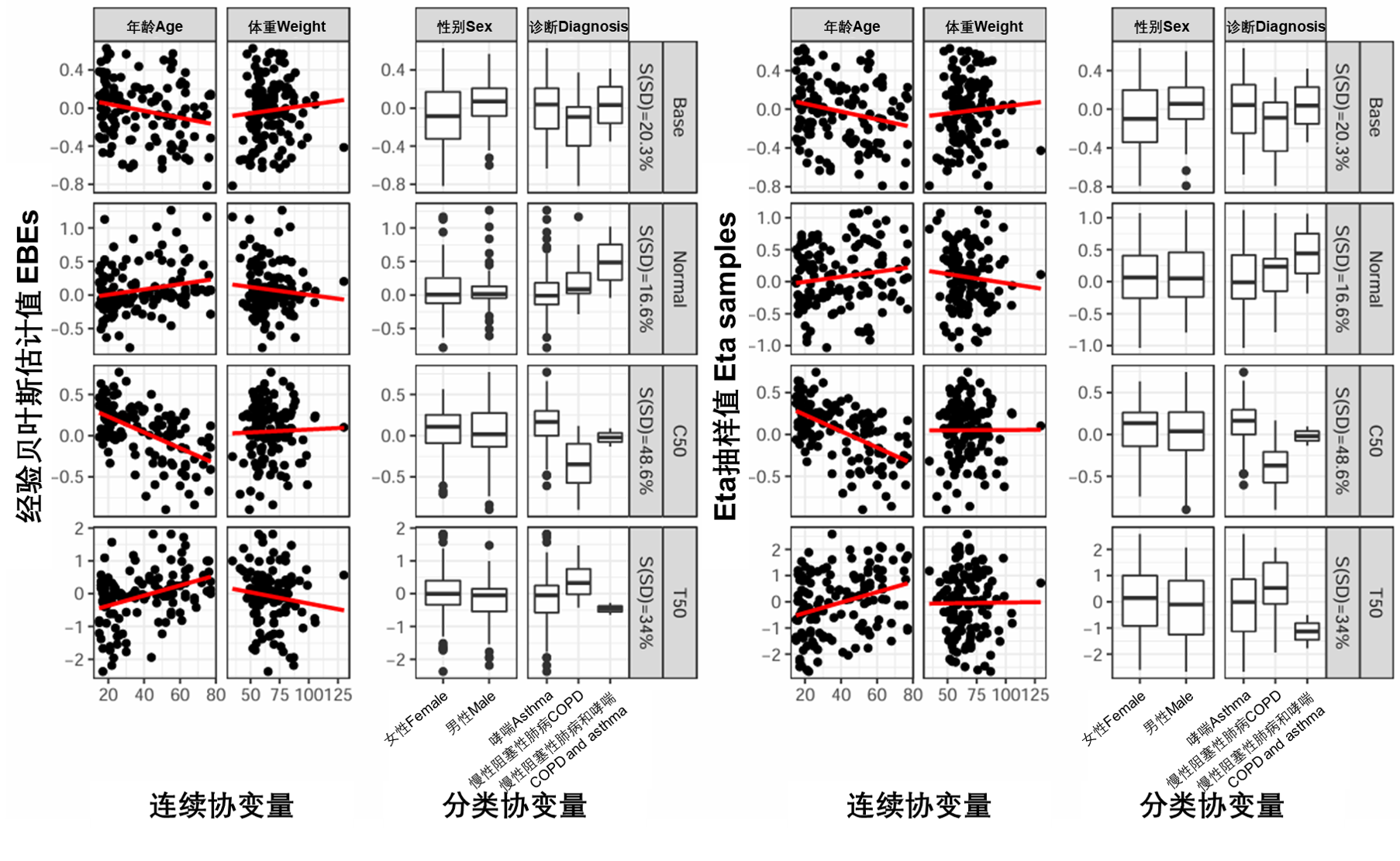图S7：EBE（左图）和etas样本（右图）与没有协变量的基础模型的协变量（run11）。连续协变量在左侧面板上使用散点图显示，红线是线性回归。分类协变量使用箱线图显示。S（SD）是根据标准差计算的收缩率。Base、Normal、C50和T50在表S3中定义。
4.2 广义加和模型 （GAM, Generalized additive model ）
广义加法模型（GAM）是在单个参数上逐步搜索协变量[5]。在Xpose4[6,7]中，在函数xpose.gam()中，使用逐步方法提供了一种实现。下面提供了一个说明示例，使用不带协变量的基础模型的残差（表S4中的run11）。
xpdb11 <- xpose4::xpose.data(runno = 11,# Read base model output with xpose4
directory = "models")
xpgam <- xpose4::xpose.gam( # Run GAM
object = xpdb11, parnam = "NORMAL",
covnams = c("AGE", "WT", "SEX", "DIAG")
)
## Start: NORMAL ~ 1; AIC= 1621.422
## Step:1 NORMAL ~ AGE ; AIC= 1575.53
## Step:2 NORMAL ~ AGE + DIAG ; AIC= 1571.575
## Step:3 NORMAL ~ AGE + SEX + DIAG ; AIC= 1566.629
## Step:4 NORMAL ~ ns(AGE, df = 2) + SEX + DIAG ; AIC= 1566.61
## Call:
## gam(formula = NORMAL ~ ns(AGE, df = 2) + SEX + DIAG, data = gamdata,
## trace = FALSE)
##
## Degrees of Freedom: 131 total; 126 Residual
## Residual Deviance: 991643.3
命令xpose.gam()在Normal参数上筛选了以下协变量：年龄AGE和体重WT（连续）以及性别SEX和诊断DIAG（分类）。协变量是使用AIC标准逐步添加的。ns选项是一种非线性关系，其特征是指示的自由度的数值。在这种情况下，首先包含AGE，首先是线性关系，然后是DIAG和SEX，然后允许年龄两个自由度。可以使用函数xp.summary()访问更详细的摘要，如下所示，包括参数估计。
xpose4::xp.summary(xpgam)
##
## SUMMARY
## Call: gam(formula = NORMAL ~ ns(AGE, df = 2) + SEX + DIAG, data = gamdata,
## trace = FALSE)
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -174.33 -64.82 10.59 51.91 280.08
##
## (Dispersion Parameter for gaussian family taken to be 7870.185)
##
## Null Deviance: 1620295 on 131 degrees of freedom
## Residual Deviance: 991643.3 on 126 degrees of freedom
## AIC: 1566.61
##
## Number of Local Scoring Iterations: 2
##
## Anova for Parametric Effects
## Df Sum Sq Mean Sq Fvalue Pr(>F)
## ns(AGE, df = 2) 2 493384 246692 31.3451 8.936e-12 ***
## SEX 1 29667 29667 3.7696 0.054425 .
## DIAG 2 105601 52800 6.7089 0.001703 **
## Residuals 126 991643 7870
## ---
## Signif. codes: 0 ’***’ 0.001 ’**’ 0.01 ’*’ 0.05 ’.’ 0.1 ’ ’ 1
##
##
## PATH TO FINAL MODEL
## Stepwise Model Path
## Analysis of Deviance Table
##
## Initial Model:
## NORMAL ~ 1
##
## Final Model:
## NORMAL ~ ns(AGE, df = 2) + SEX + DIAG
##
## Scale: 12368.67
##
## From To Df Deviance Resid. Df Resid. Dev AIC
## 1 <start> 131 1620295.4 1621.422
## 2 AGE -1 -493034.2 130 1127261.2 1575.530
## 3 DIAG -2 -65921.9 128 1061339.3 1571.575
## 4 SEX -1 -54412.6 127 1006926.7 1566.629
## 5 aGE ns(AGE, df = 2) -1 -15283.4 126 991643.3 1566.610
##
## COEFFICIENTS
## (Intercept) ns(AGE, df = 2)1 ns(AGE, df = 2)2 SEX1
## 75.16201 -187.79854 -80.36751 43.67164
## DIAG2 DIAG3
## -106.94693 -48.29317
##
## PRERUN RESULTS
## Dispersion:
##
## DATA
## Subset expression:
## Only first value of covariate considered
## for each individual: TRUE
## Covariates normalized to median: TRUE
图S8提供了逐步搜索的图示，其中所有尝试的残差模型都根据其赤池信息判据（AIC）进行排序。图S9中提供了所选协变量与筛选参数的基础模型（run11）残差之间的相关性图示。
数字对应于受试者唯一标识符，并允许发现异常值。用于生成这两个图的R代码可在附录B.9中找到。
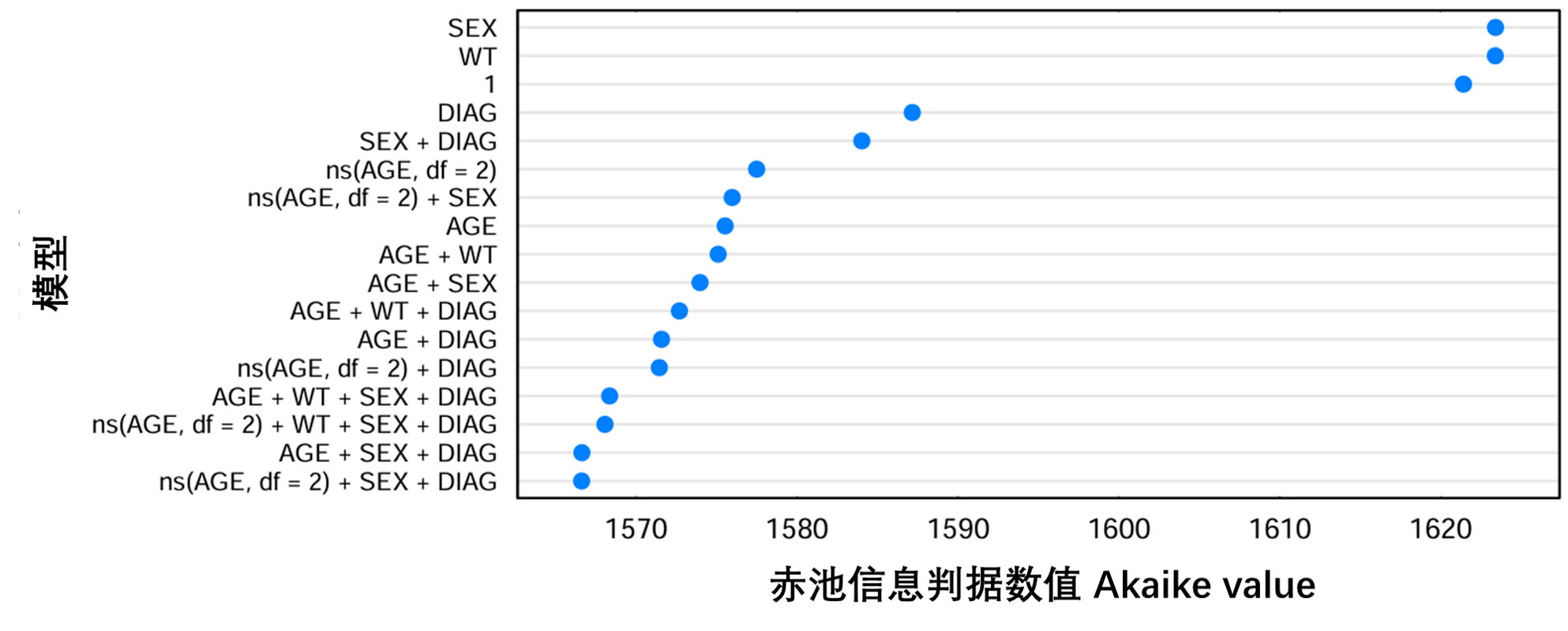图S8：在Normal上逐步搜索基础模型（run11）的每个模型的赤池信息判据值。名为1的模型是不带协变量的模型。
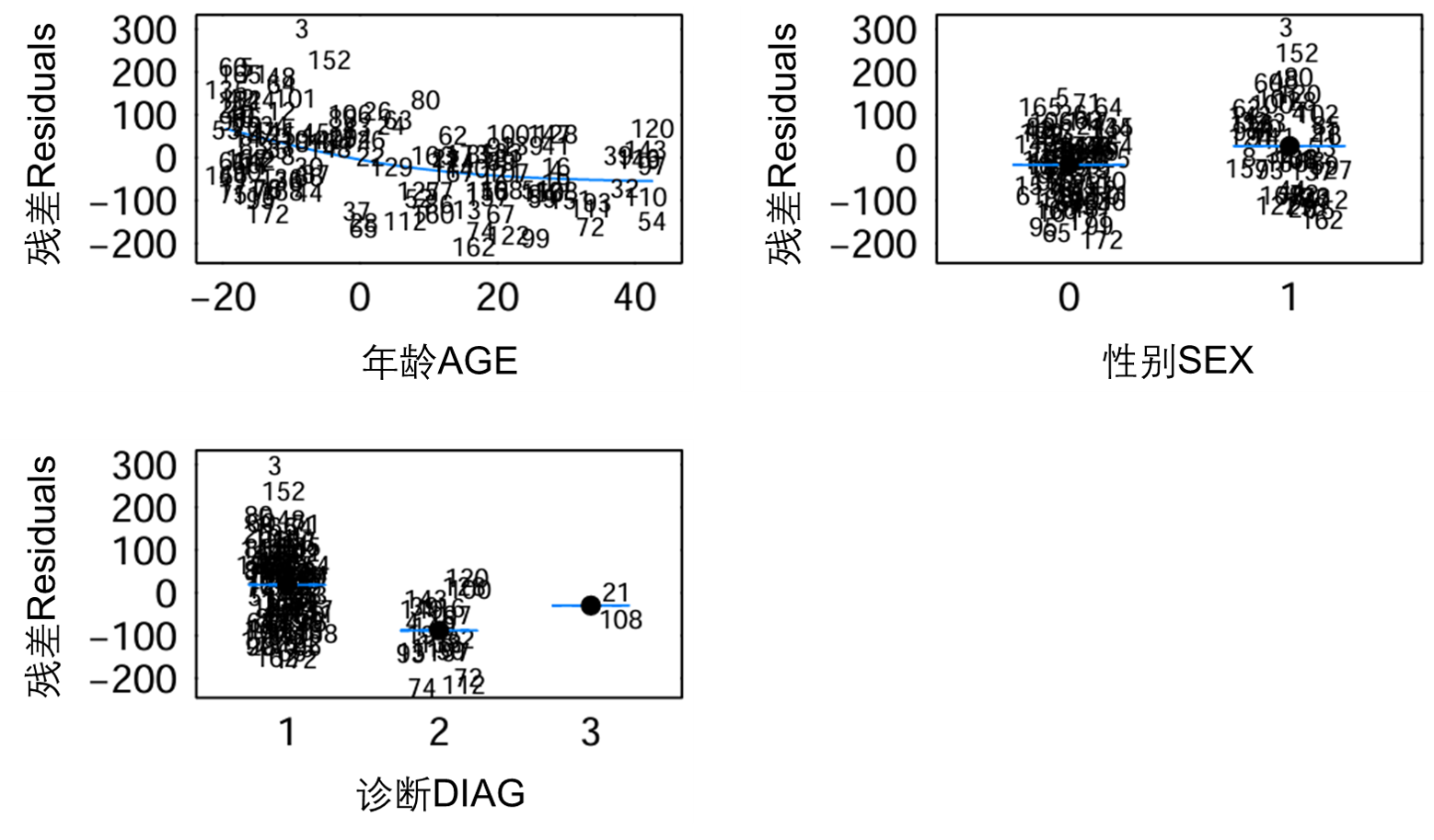图S9：基础模型（run11）中Normal参数的残差对GAM所选协变量的协变量。这些数字对应于受试者唯一标识符。
4.3 瓦尔德近似法(WAM, Wald approximation method)
WAM的起点是FFEM，它包含所有考虑的参数-协变量关系，这些关系被建模为固定效应。协变量效应如图S5所示。如前所述，FFEM仅限于Base和Normal上的饱和协变量模型。附录A.3中提供了NONMEM代码。
协变量固定效应的不确定性由NONMEM协方差步骤获得。使用协变量的固定效应估计值和不确定性这两个信息，可以近似计算出每个简化的子模型和FFEM之间的OFV差异。因此，瓦尔德近似法(WAM)是似然比检验（LRT）的近似。然后可以根据aLRT（近似LRT）进行模型选择，选择具有最低aLRT值和较少参数的模型。然而，由于aLRT是一个近似值，因此建议将”施瓦茨贝叶斯判据(SBC，Schwarz’s Bayesian criterion)”作为选择标准，以支持更简洁的模型[8]，选择具有最高SBC值的模型。然后，建议通过运行WAM建议的15个最佳模型来检查近似假设，以比较和检查真实LRT和SBC与近似模型之间的相关性。
用于计算FFEM（run22）的所有协变量子模型的LRT统计量的Wald近似值的R代码可在附录B.10中找到。结果如表S6所示。在与该FFEM的2k个可能的协变量模型相对应的256行中，仅显示表的前15行（即根据SBC标准的15个最佳模型）。
SBC建议的最终协变量模型在表S6中排名第一，在NONMEM中运行（表S4中的run24，附录A.4中提供的NONMEM代码），与FFEM模型相比，删除了4个协变量效应的模型的OFV增加了+23点。相应的χ2阈值为9.49（α=0.05）。
表S6：使用FFEM拟合的WAM选择方法的结果（run22）。假设的受限模型根据SBC进行排序，仅显示表格的前15行。
| 排序 | 包含的协变量参数 | 近似似然比检验(aLRT) | 施瓦茨贝叶斯判据(SBC) |
|---|---|---|---|
| 1 | Sex on Base, Age on Base, Diag on Normal, Age on Normal | 9.74 | -51.86 |
| 2 | Sex on Base, Age on Base, Age on Normal | 16.61 | -52.16 |
| 3 | Sex on Base, Age on Base, WT on Base, Diag on Normal, Age on Normal | 5.94 | -53.09 |
| 4 | Sex on Base, Age on Base, WT on Base, Age on Normal | 12.74 | -53.36 |
| 5 | Sex on Base, Age on Base, Diag on Normal, Sex on Normal, Age on | 6.66 | -53.45 |
| 6 | Sex on Base, Diag on Normal, Age on Normal | 20.16 | -53.94 |
| 7 | Diag on Normal, Sex on Normal, Age on Normal | 20.34 | -54.03 |
| 8 | Sex on Base, Age on Normal | 26.77 | -54.11 |
| 9 | Sex on Base, Age on Base, Diag on Normal, Age on Normal, WT on Normal | 8.16 | -54.20 |
| 10 | Diag on Normal, Sex on Normal, Age on Normal, WT on Normal | 14.76 | -54.37 |
| 11 | Age on Base, Diag on Normal, Sex on Normal, Age on Normal, WT on Normal | 8.61 | -54.43 |
| 12 | Age on Base, Diag on Normal, Sex on Normal, Age on Normal | 15.27 | -54.62 |
| 13 | Diag on Base, Sex on Base, Diag on Normal, Age on Normal | 15.46 | -54.72 |
| 14 | Sex on Base, Age on Base, Age on Normal, WT on Normal | 15.63 | -54.81 |
| 15 | Diag on Base, Sex on Base, Age on Base, Diag on Normal, Age on Normal | 9.42 | -54.83 |
aLRT：近似似然比统计量，SBC：施瓦茨贝叶斯判据，Schwarz’s Bayesian criterion。
4.4 逐步协变量建模(SCM, Stepwise covariate modelling)
SCM（逐步协变量模型）方法包括对模型的协变量效应的前向选择和向后消除。简而言之，每个相关参数-协变量关系的一个模型以单变量方式进行检验。在第一步中，根据某些条件提供最佳数据拟合的模型将被保留并推进到下一步。在以下步骤中，将测试所有剩余的参数协变量组合，直到没有更多的协变量满足包含在模型中的标准。“前向选择”（Forward Selection）之后可以进行“后向消除”（Backward Elimination），后者将作为前向选择进行，但反过来，使用更严格的模型改进标准。PsN[9,10]中的函数scm中提供了一个实现。下面给出了一个使用PsN实现的应用示例。
由于运行 SCM 有许多选项，因此在命令行上指定所有选项是不切实际的，因此 PsN 要求用户编写一个以 .scm 扩展名保存的专用配置文件。然后，可以使用以下命令运行 SCM 配置：
scm -config_file=theophylline.scm
下面提供了“茶碱（theophylline）”数据配置文件的示例，称为theophylline.scm，使用不带协变量的基础模型（表S4中的run11）作为起点，以在所有固定效应参数上筛选所有可用协变量。有关详细信息，请参阅PsN文档（https://uupharmacometrics.github.io/PsN/docs.html）。
## model=run11.mod
## search_direction=both
## p_forward=0.05
## p_backward=0.01
##
## continuous_covariates=AGE,WT
## categorical_covariates=SEX,DIAG
##
## [test_relations]
## BASE=AGE,WT,SEX,DIAG
## NORMAL=AGE,WT,SEX,DIAG
## T50=AGE,WT,SEX,DIAG
## C50=AGE,WT,SEX,DIAG
##
## [valid_states]
## continuous = 1,2,3,4,5
## categorial = 1,2,3,4,5
PsN以多种格式输出SCM选择的结果，其中选择两种格式来说明该方法。第一个图示表示在前向搜索过程中每个步骤实现的OFV下降，如图S10所示（附录B.11.1中提供的R代码）。选择的第二个输出是总结整个SCM搜索（scmlog.txt）和最终模型中包含的最终参数协变量关系的文本文件，可在附录B.11.2中找到。
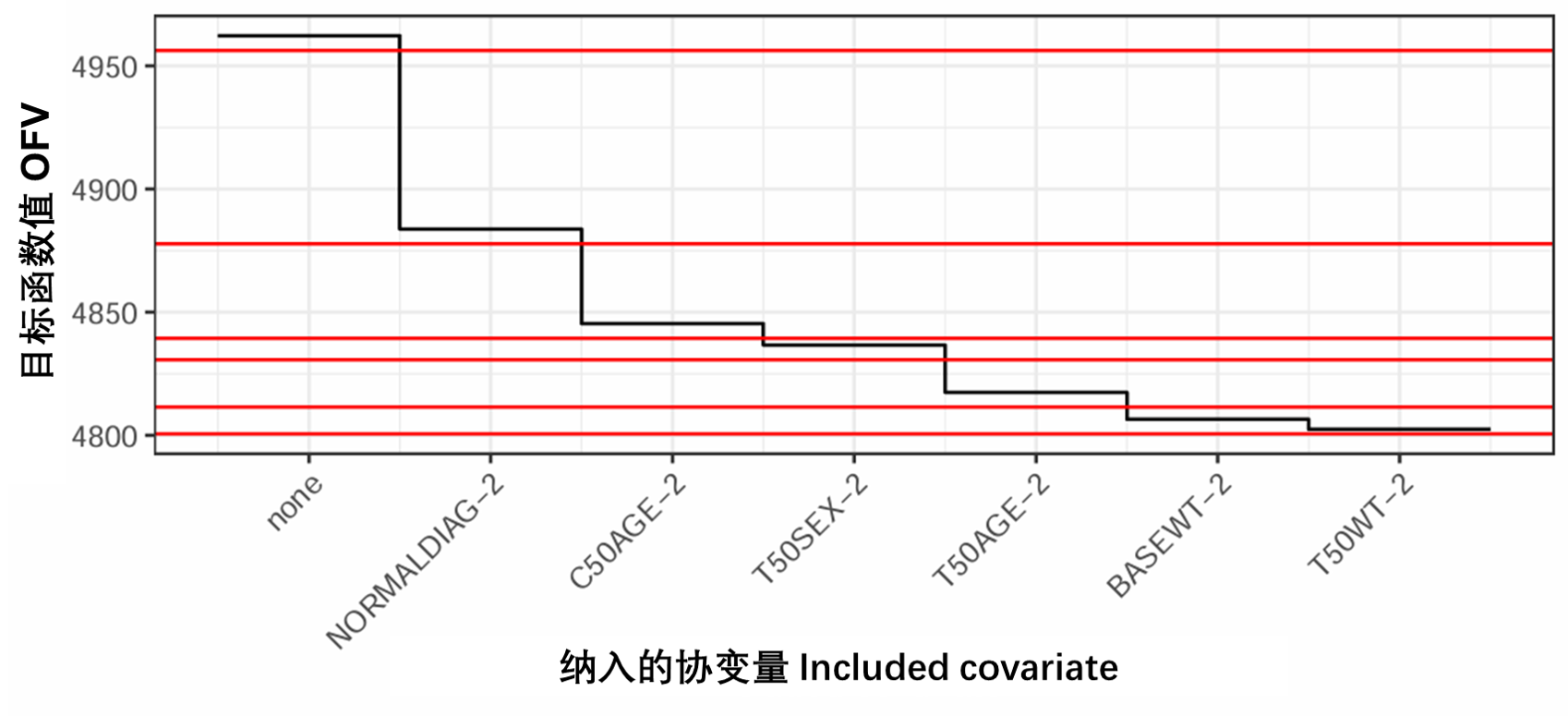图S10：与所选参数-协变量选择关联的SCM前向搜索的每个步骤的OFV下降。Base、Normal、C50和T50在表S3中定义。红线对应于每个步骤的显著性阈值。
下面的代码显示了与没有协变量的基础模型相比，最终SCM模型中添加的代码行，这显示了协变量是如何包含在模型中的。完整的NONMEM代码可在附录A.6中找到。
## > $THETA (-0.016,0.00557403,0.032) ; BASEWT1
## > $THETA (-0.024,0.0226863,0.051) ; C50AGE1
## > $THETA (-1,-0.496745,5) ; NORMALDIAG1
## > (-1,-0.2698,5) ; NORMALDIAG2
## > $THETA (-0.024,0.0442177,0.051) ; T50AGE1
## > $THETA (-1,-0.780861,5) ; T50SEX1
## > $THETA (-0.016,-0.0129475,0.032) ; T50WT1
## > $OMEGA 0.118039 ; IIV_BASE
## > 0.0044012 ; IIV_NORMAL
## > 2.8273 ; IIV_T50
## > 0.328448 ; IIV_C50
## > $SIGMA 0.0249899 ; RUV_PROP
## > T50WT = ( 1 + THETA(13)*(WT - 66))
## > IF(SEX.EQ.0) T50SEX = 1 ; Most common
## > IF(SEX.EQ.1) T50SEX = ( 1 + THETA(12))
## > T50AGE = ( 1 + THETA(11)*(AGE - 34.5))
## > T50COV=T50AGE*T50SEX*T50WT
## > IF(DIAG.EQ.1) NORMALDIAG = 1 ; Most common
## > IF(DIAG.EQ.2) NORMALDIAG = ( 1 + THETA(9))
## > IF(DIAG.EQ.3) NORMALDIAG = ( 1 + THETA(10))
## > NORMALCOV=NORMALDIAG
## > C50AGE = ( 1 + THETA(8)*(AGE - 34.5))
## > C50COV=C50AGE
## > BASEWT = ( 1 + THETA(7)*(WT - 66))
## > BASECOV=BASEWT
## > TVBASE = BASECOV*TVBASE
## > TVNORMAL = NORMALCOV*TVNORMAL
## > TVT50 = T50COV*TVT50
## > TVC50 = C50COV*TVC50
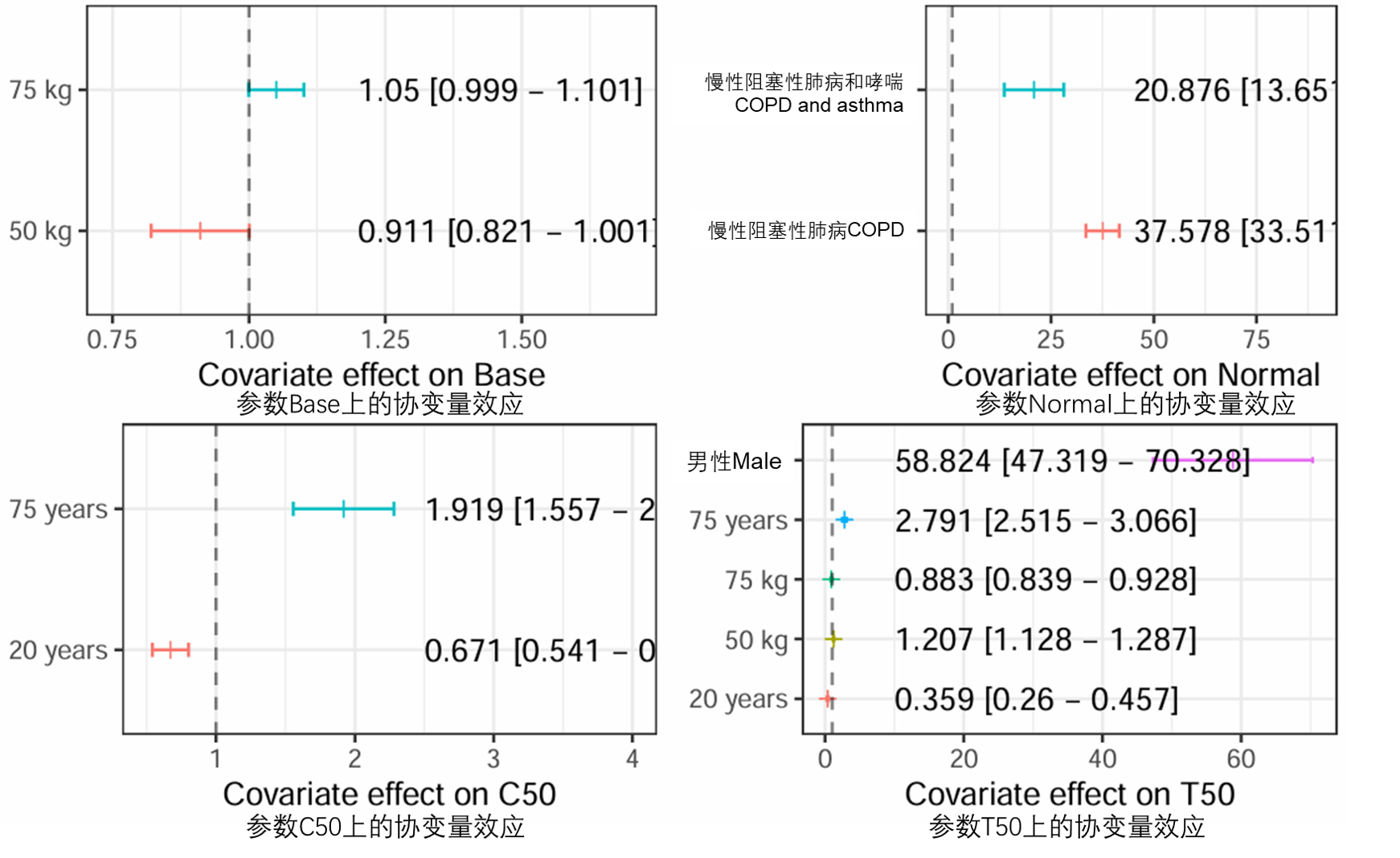图S11：森林图，表示协变量对基于已发布模型（run20）的Normal参数的影响，相对于数据集中的典型参与者（患有哮喘的40岁男性），由垂直虚线表示。条形符号表示适用子群体类别的Normal值中位数，胡须表示基于SIR不精确估计值的中值的95%置信区间。相应的具体数值显示在右侧。
4.5 最小绝对收缩和选择算法（LASSO, The Least absolute shrinkage and selection operator）
群体药代动力学和药效动力学的协变量模型通常采用逐步协变量建模程序构建。在分析小型数据集时，这种方法可能会产生一个协变量模型，该模型存在选择偏差和较差的预测性能。LASSO工具[11]是解决这些问题的方法。它也可能比SCM工具更快，并提供协变量模型的验证。
在LASSO工具中，所有协变量必须标准化为均值为零，标准差为1。随后，包含所有潜在协变量-参数关系的模型具有一个限制：绝对协变量系数的总和必须小于值t。该限制将迫使某些系数趋于零，而其他系数则通过收缩来估计。在实践中，这意味着在拟合模型时，在估计包含关系的同时测试协变量关系是否包含。对于给定的SCM分析，模型大小取决于选择所需的p值。在LASSO工具中，模型大小取决于t的值，该值可以使用交叉验证进行估计。LASSO方法在PsN中实现[9,10]，包括估计t值所需的交叉验证步骤。下面给出了一个使用PsN实现的应用示例。图S12说明了如何根据交叉验证结果选择最佳t值。
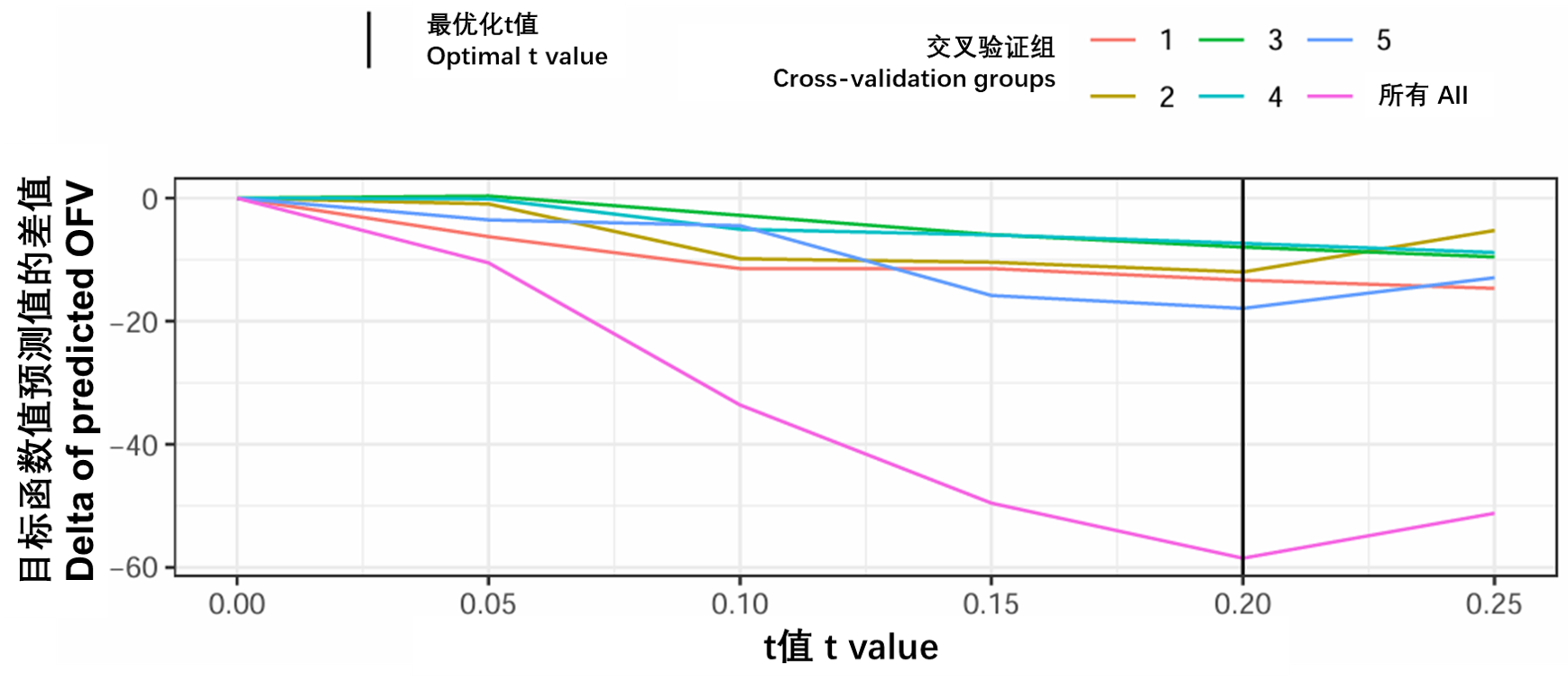图S12：五个交叉验证组中每个组的预测OFV和五个组的总和。
每个参数（例如NORMAL）与强制选项-relations一起列出，其典型值必须编码为模型中的TV参数，例如TVNORMAL。协变量效应将以乘法方式添加到TV变量中。在下面的代码中，年龄和体重（连续，命令中用-2表示）以及性别和诊断（分类，命令中用-1表示）在基础模型的normal参数上进行测试（参见第3.2节）。
lasso run11.mod -dir=lasso_run11_normal -relations=NORMAL:AGE-2,WT-2,SEX-1,DIAG-1
此命令的主要输出如表S7所示。
表S7：用LASSO测试的感兴趣参数（NORMAL）的参数的最终系数。
| NORMALAGE | NORMALDIAG2 | NORMALDIAG3 | NORMALSEX1 | NORMALWT | FACTOR | CONVERGED |
|---|---|---|---|---|---|---|
| -0.0512465 | -0.1487535 | 0 | 0 | 0 | 1.000057 | 1 |
系数为0表示未选择协变量。FACTOR是应用于变量的校正因子，以确保添加协变量效应的绝对值的和与t值之间的比率等于1。CONVERGED表示最终协变量模型收敛。
下面的代码显示了添加到不带协变量的基础模型中的代码行，以及如何将协变量包含在模型中。
## > $THETA (-0.49650,0.0001,0.79798) ; TH7 NORMALAGE
## > $THETA (-0.44892,0.0001,2.24459) ; TH8 NORMALDIAG2
## > $THETA (-0.12451,0.0001,8.09297) ; TH9 NORMALDIAG3
## > $THETA (-0.78384,0.0001,1.28550) ; TH10 NORMALSEX1
## > $THETA (-0.23442,0.0001,0.44966) ; TH11 NORMALWT
## > $THETA (-1000000,0.2) FIX ; TH12 T-VALUE
## > $OMEGA 0.164643 ; IIV_BASE
## > 0.160737 ; IIV_NORMAL
## > 1.59823 ; IIV_T50
## > 0.41132 ; IIV_C50
## > $SIGMA 0.0190902 ; RUV_PROP
## > $PRED
## > ;;; LASSO-BEGIN
## > TVALUE = THETA(12)
## > ABSSUM = aBS(THETA(7))+ABS(THETA(8))+ABS(THETA(9))+ABS(THETA(10))
## > ABSSUM = aBSSUM+ABS(THETA(11))
## >
## > RATIO = ABSSUM/TVALUE
## > IF (RATIO .GT. 5) EXIT 1 1
## > FACTOR = EXP(1-RATIO)
## >
## > DIAG2 = 0
## > DIAG3 = 0
## > SEX1 = 0
## > IF (DIAG .EQ. 2) DIAG2=1
## > IF (DIAG .EQ. 3) DIAG3=1
## > IF (SEX .EQ. 1) SEX1=1
## >
## > NORMALAGE = THETA(7)*(AGE-38.78030)/18.97621*FACTOR
## > NORMALDIAG2 = THETA(8)*(DIAG2-0.16667)/0.37410*FACTOR
## > NORMALDIAG3 = THETA(9)*(DIAG3-0.01515)/0.12262*FACTOR
## > NORMALSEX1 = THETA(10)*(SEX1-0.37879)/0.48693*FACTOR
## > NORMALWT = THETA(11)*(WT-67.22576)/14.71551*FACTOR
## >
4.6 全随机效应模型（FREM, Full random effect model）
使用FREM[12‒14]选择感兴趣的协变量时无需考虑它们的相关性。协变量作为观测变量输入到数据集中，其多变量分布被建模为随机效应。参数和协变量的随机效应之间的全协方差矩阵与其他模型组件一起估计。FREM方法是在PsN中实现的[9,10]，下面给出了一个使用PsN实现的应用示例。使用了以下命令：
frem run11.mod -covariates=SEX,WT,AGE,DIAG -categorical=SEX,DIAG -dir=frem_run11 -bipp
森林图（图S13）说明了估计的协变量效应，表示为每个参数的效应大小（以百分比为单位）及其不确定性。这类曲线图通常用于说明预先指定的协变量方法的任何协变量效应，其中置信度区间不受选择偏倚的影响。在这个例子中，慢性阻塞性肺病和哮喘诊断类别只有两个人，导致参数具有非常高的不确定性（值>1e+20）。绘制这些值不是为了保持绘图的其余部分可读性。
最终的FREM模型代码在附录A.7中提供。用于创建图S13和图S14的数据在PsN生成的文件夹中找到，并根据附录中提供的代码进行处理。
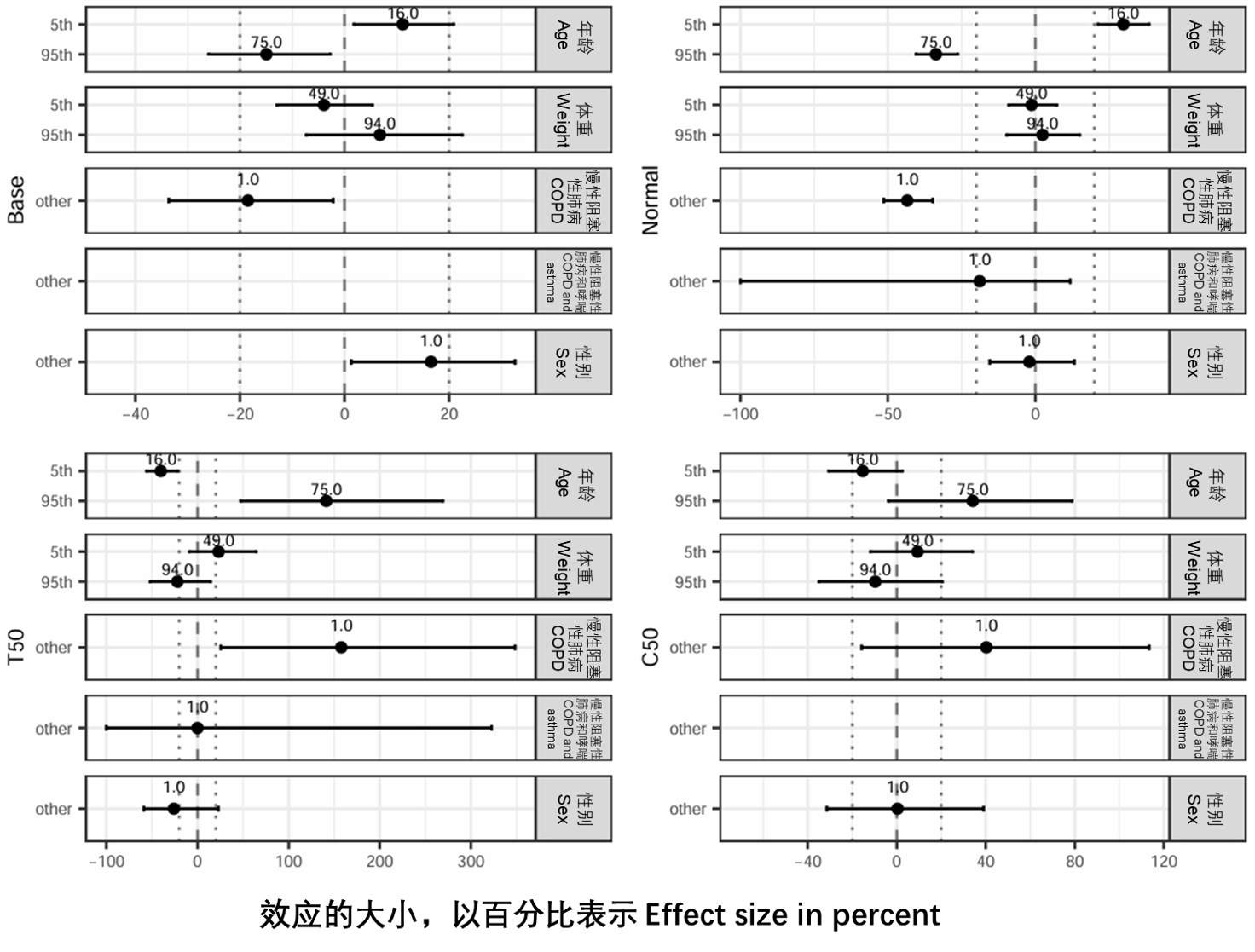图S13：协变量效应，以百分比表示，每个参数和协变量都有不确定性。这些数字是第5个和第95个百分位数的协变量值，虚线是无效线虚线划定了临床无关区域(±20%)。没有绘制无限大的值，导致面为空。Base、Normal、C50和T50在表S3中定义。
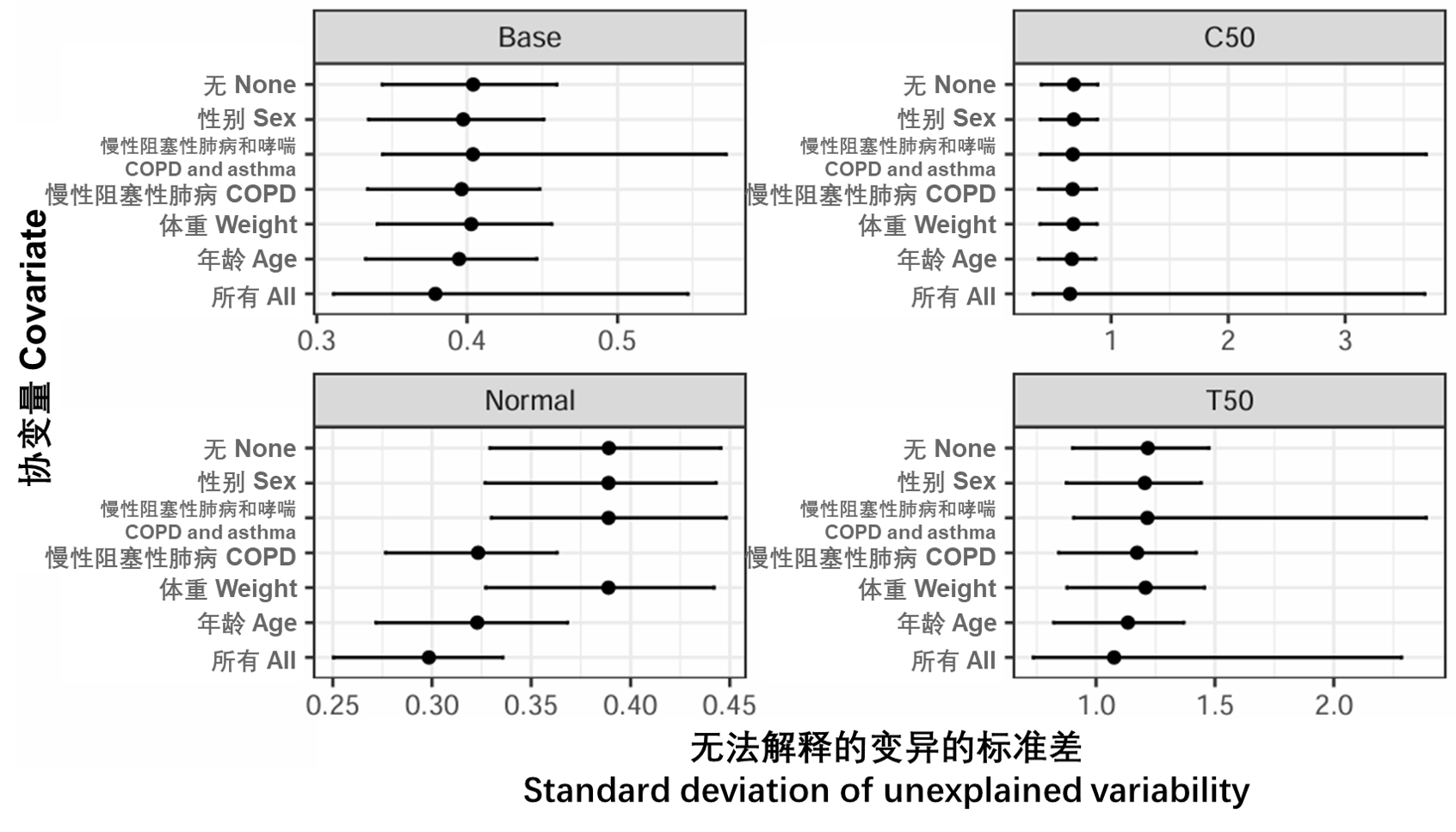图S14：所有参数和协变量组合的原始无法解释的变异性以及不确定性。点是观测到的标准差（SD），条形表示第5和第95个SD不确定度。Base、Normal、C50和T50在表S3中定义。
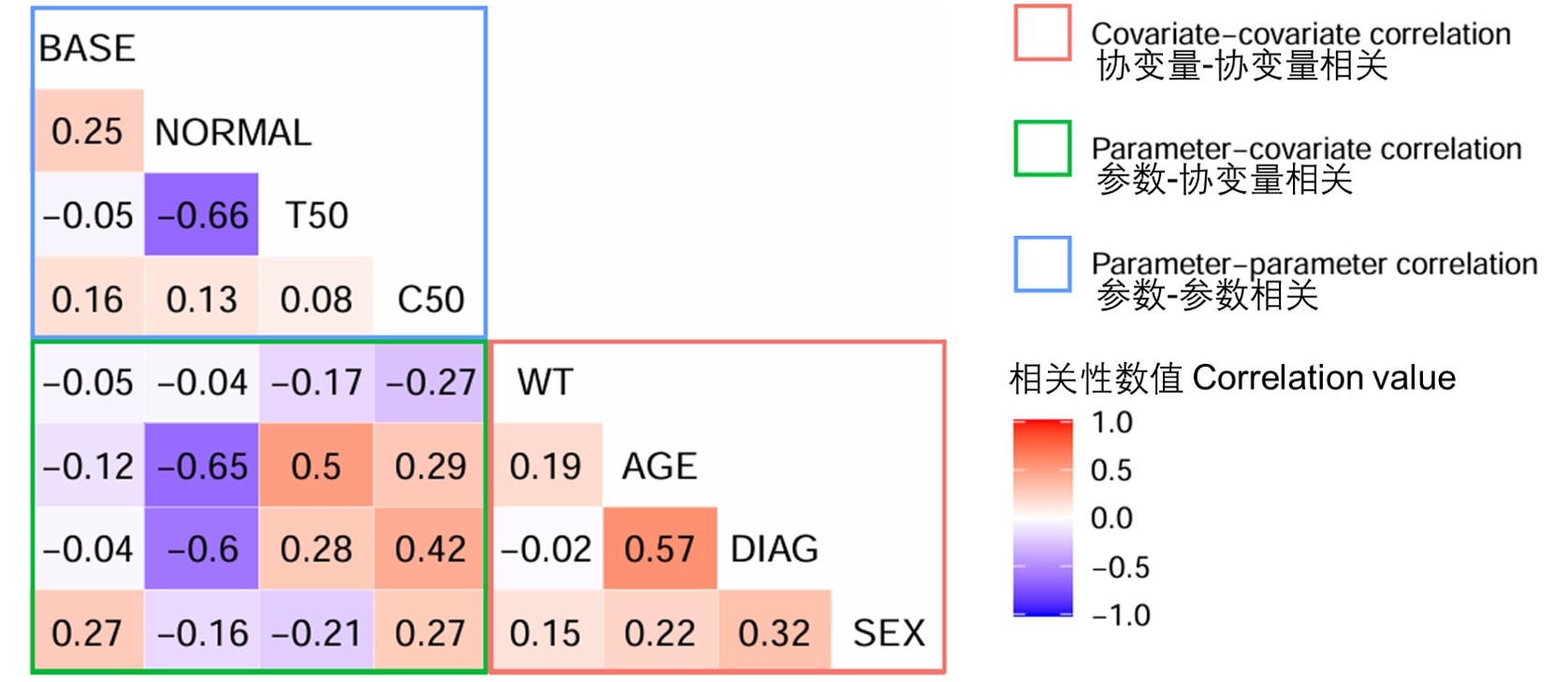图S15：来自FREM模型的相关矩阵（run28）。
5 协变量效应的模型诊断
本节提供了如何使用VPC和EBE-协变量关系图诊断协变量效应的示例。值得注意的是，VPC区间被认为具有不同的名称[15,16]。
图S16显示了没有协变量的模型（表S4中的run11）和通过运行SCM获得的协变量模型（表S4中的run25）之间的VPC有所改善。在这种情况下，协变量纳入改善了对最高观测值的预测，因为第95个预测百分位数的95%CI更窄，观测值的中位数也得到了更好的预测。
图S17显示了与图S16相同的VPC，但根据年龄协变量分层，该协变量包含在使用SCM获得的协变量模型中，使用中位年龄创建两个年龄类别。分层强调，年轻个体的PEFR较高，并且每个类别的典型观测值中位数不是在预测区间的极端值，而是协变量的纳入导致预测区间中位数更好地以中位观测值为中心。附录B.14详细介绍了如何创建不同的VPC。
图S18显示了纳入协变量之前(左图)和之后(右图)作为年龄协变量函数的PEFR预测。结果表明，在协变量纳入后，PEFR对年龄的依赖性可以更好地预测。中位预测区间更好地以观测值为中心，最老个体的PEFR和最高PEFR值的预测效果更好。在所介绍的三种不同VPC中，基于SCM的协变量模型的不精确性和拟合度都得到了改善。
图S19显示了在包含协变量之前(左图)和之后(右图)作为茶碱浓度函数的PEFR预测。SCM协变量效应估计对PEFR的中位预测没有任何明显影响，但确实有助于将预测的上半分位数和下限更接近观察到的百分位数。这一模式支持选择茶碱效应的Emax药效动力学模型，但无法确定SCM确定的协变量或协变量组合解释了受试者之间的变异性。应用FREM方法(图S13)确定的T50的年龄和诊断将是一个起点，看看这两个协变量是否有助于预测VPC的变异性。T50参数描述了气道阻塞的恢复速度，随着年龄的增长和COPD，预计恢复速度会更长。
还可以检查纳入协变量前后EBEs-协变量关系的差异(图S7)。预期的模式是EBE和协变量之间的相关性降低。图S20显示了按照SCM方法（run25）包含协变量后的EBE-协变量关系。线性回归趋势被扁平化，表明现有的相关性现在包含在模型中。有关SCM协变量模型的详细信息，请参见第4.4节。
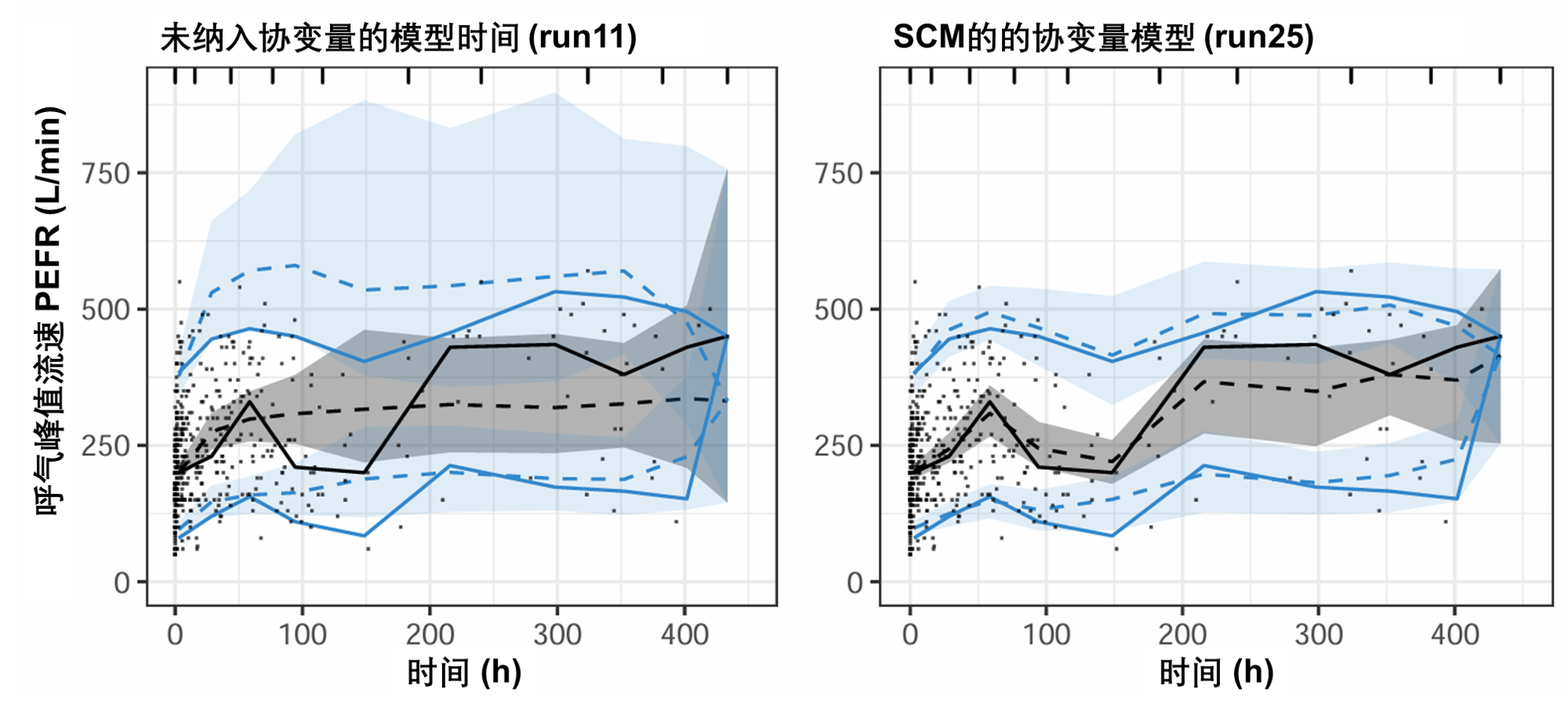图S16：PEFR对时间曲线的可视化预测检验图。该图基于500次模拟。虚线和阴影区域表示模型模拟的中位数、第5个和第95个百分位数及其相应的95%置信区间。实线表示观测数据的中位数、第5个和第95个百分位数。PEFR：峰值呼气流速。
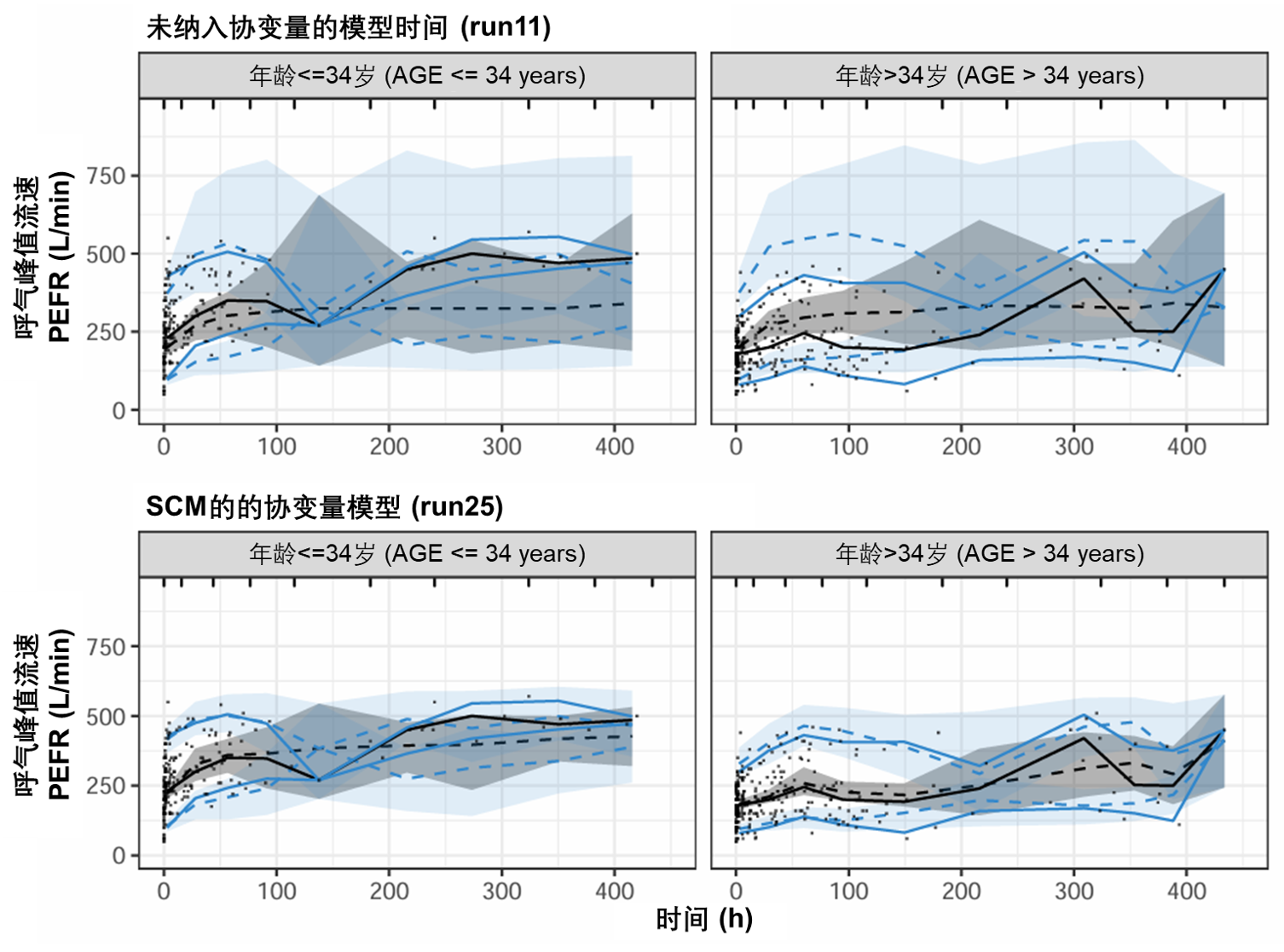图S17：PEFR对时间曲线在协变量纳入之前（顶部）和之后（底部）的可视化预测检验图，根据年龄协变量分层。该图基于500次模拟。虚线和阴影区域表示模型模拟的中位数、第5个和第95个百分位数及其相应的95%置信区间。实线表示观测数据的中位数、第5个和第95个百分位数。PEFR：峰值呼气流速。
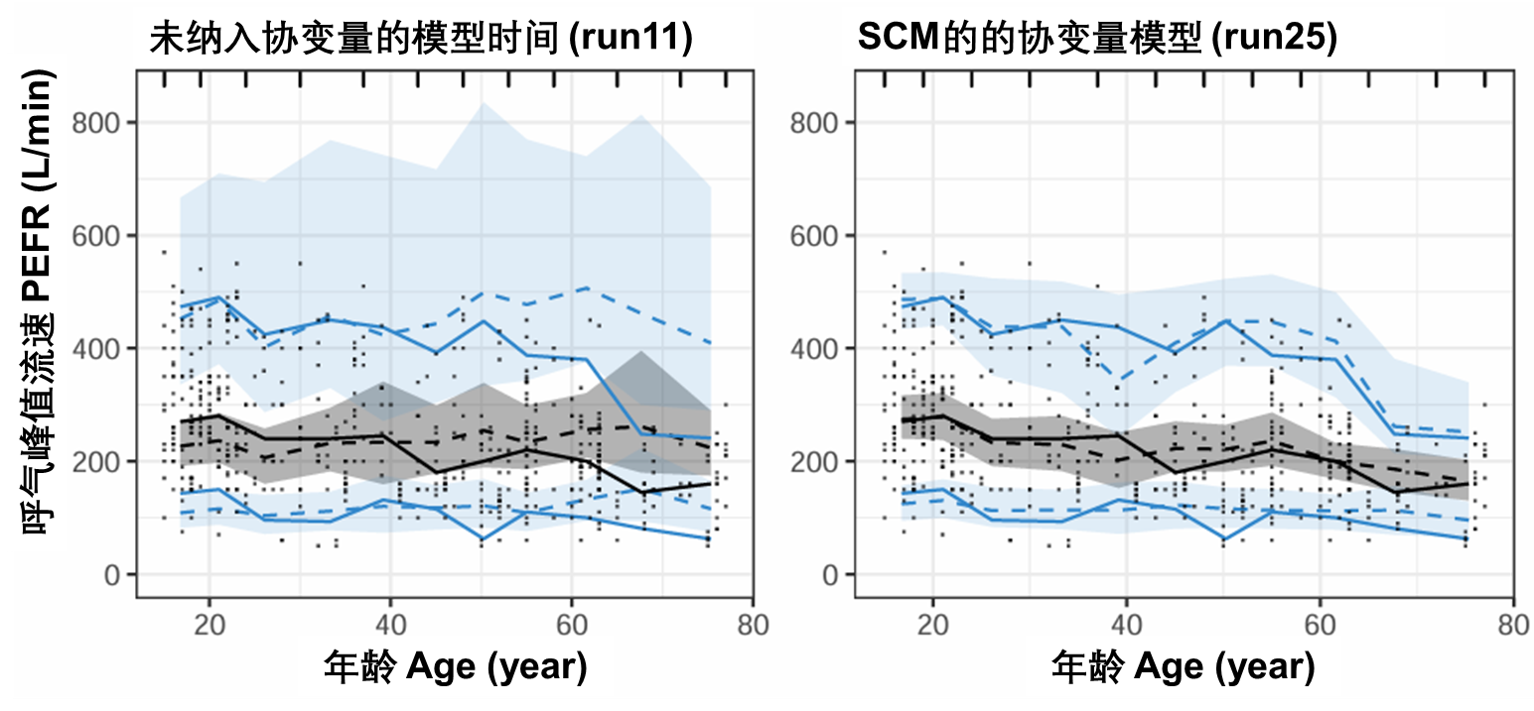图S18：PEFR对年龄的可视化预测检验图。该图基于500次模拟。虚线和阴影区域表示模型模拟的中位数、第5个和第95个百分位数及其相应的95%置信区间。实线表示观测数据的中位数、第5个和第95个百分位数。PEFR：峰值呼气流速。
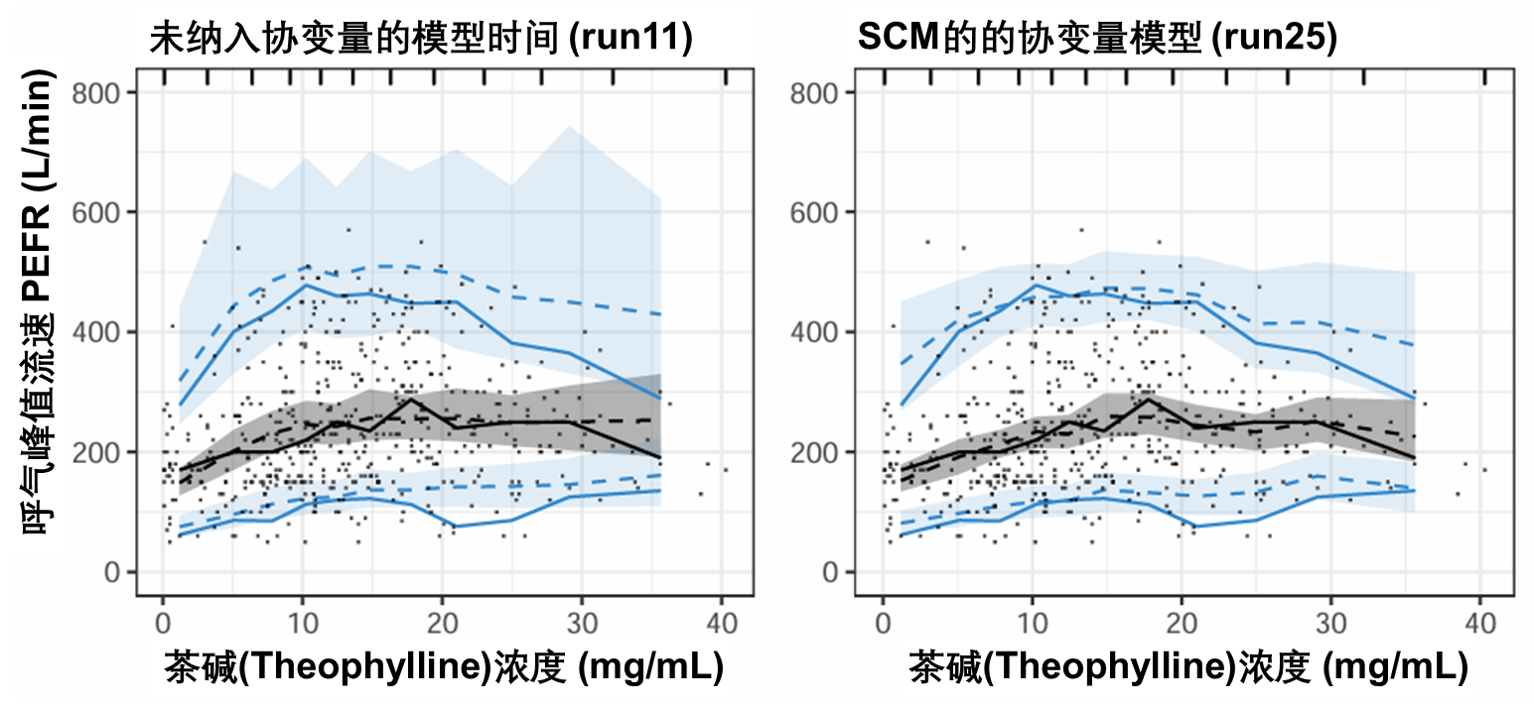图S19：PEFR对茶碱浓度的可视化预测检验图。该图基于500次模拟。虚线和阴影区域表示模型模拟的中位数、第5个和第95个百分位数及其相应的95%置信区间。实线表示观测数据的中位数、第5个和第95个百分位数。PEFR：峰值呼气流速。
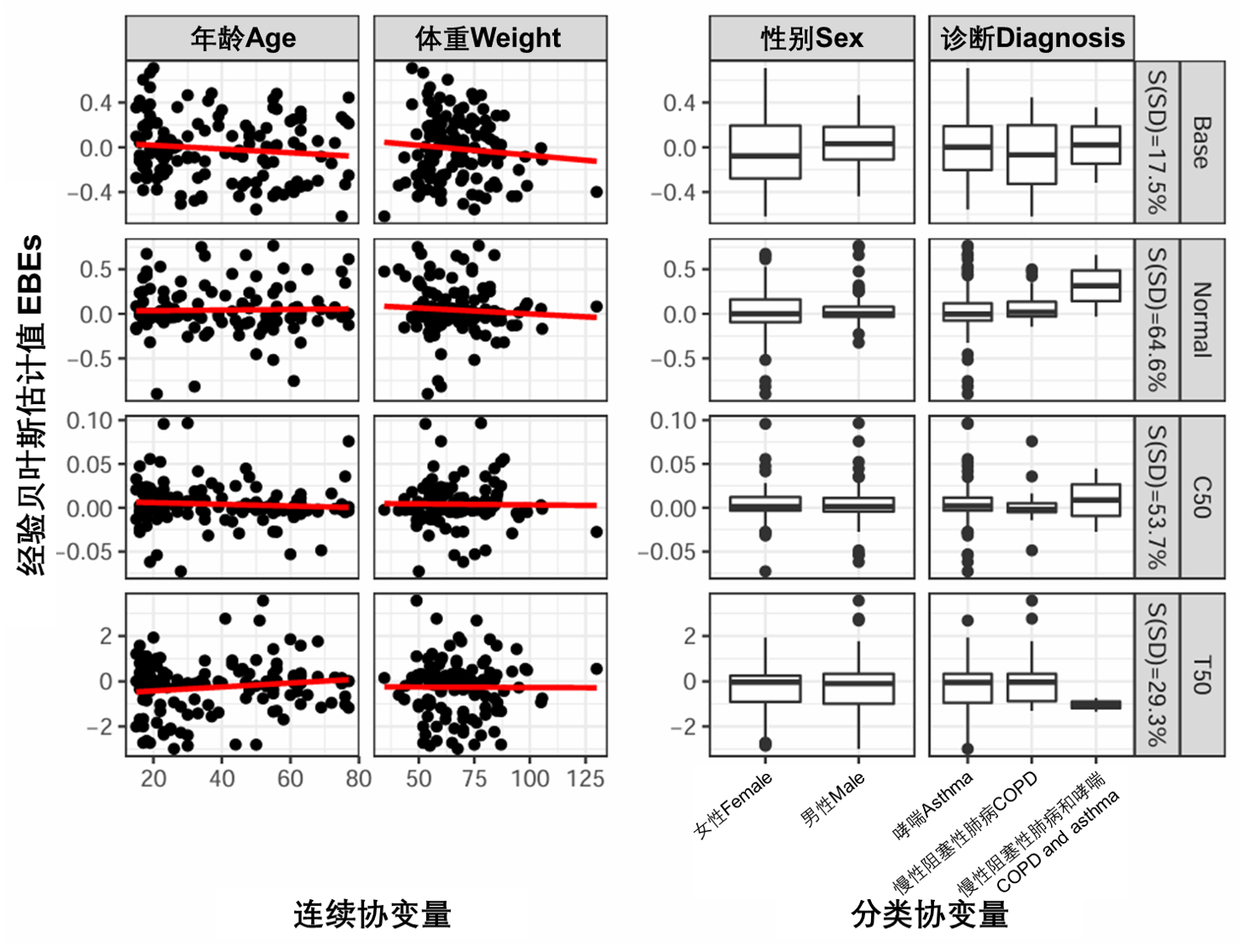图S20：基于SCM的协变量模型的EBE与协变量（run25）。连续协变量在左侧面板上使用散点图显示，红线是线性回归。分类协变量使用箱线图显示。S（SD）是根据标准差计算的收缩率。Base、Normal、C50和T50在表S3中定义。
6 协变量效应总结和报告
本节旨在提供一个示例，说明如何使用协变量模型和出版物的结果（表S4中的run20）总结和报告模型中包含的协变量效应。
协变量模型构建过程后获得的模型介绍如下。表S8提供了协变量模型(run20)与没有协变量的模型(run11)的未变换最终估计，包括IIV参数的RSE和收缩。两个模型的RSE均通过SIR（重要性重抽样，sampling importance resampling）获得。一位40岁男性哮喘患者入院时的PEFR（Base）估计值为136L/min，预测完全恢复值的PEFR为481L/min。支气管狭窄因子的半衰期为19.6小时。茶碱的最大作用是产生与时间相关的最大效应的37.3%（ε_theo）。8.48mg/L的浓度可达到茶碱50%的潜在效应。曲线的陡峭程度用2.59的指数来描述。通过修改Normal参数的诊断、年龄和性别方面的，模型预测得到了明显改善。Normal参数随着COPD的诊断而增加，女性通常较低，并且与年龄成反比。
纳入协变量后，除了Normal参数、T50参数和Normal参数的IIV外，其他参数都发生了微小的变化。Normal参数的变化是意料之中的，因为它是被添加协变量的参数。该参数表示模型中没有协变量时的整个群体的典型值，而在纳入协变量后因为归一化关系，它表示协变量模型中子集（患有哮喘的40岁男性）的典型值。由于协变量纳入解释了群体中参数变异性的一部分，因此Normal参数的IIV也会降低。
使用图S21森林图通过图示的方式表示了所包含效应。所有协变量效应都会降低PEFR，但与较高PEFR相关的年轻年龄除外。用于创建绘图的代码在附录B.13中提供。
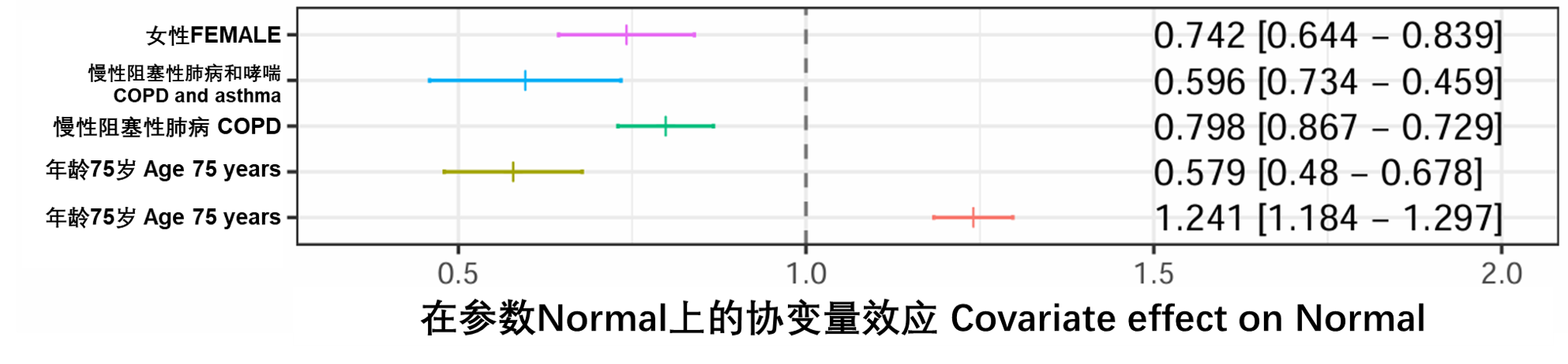图S21：森林图，表示协变量对基于已发布模型（run20）的Normal参数的影响，相对于数据集中的典型受试者（患有哮喘的40岁男性），由垂直虚线表示。条形符号表示适用子群体类别的Normal值的中位数，胡须表示基于SIR不精确估计值的中值的95%置信区间。相应的数值显示在右侧。
表S8：不带协变量的基础模型（run11）和基于已发布的协变量模型的模型（run20）的参数表。
| 无协变量的基础模型 (run11) | 基于文献的协变量模型(run20) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 参数 | 描述 | 单位 | 数值 | 相对标准误* | 收缩值 (%) | 数值 | 相对标准误* | 收缩值 (%) | |
| Base | 基线时的呼气峰值流速(PEFR) | L/min | 143 | 0.0534 | - | 136 | 0.0642 | - | |
| Normal | 在不包含支气管狭窄因子(BCF)下的呼气峰值流速(PEFR)† | L/min | 332 | 0.0546 | - | 481 | 0.0621 | - | |
| T50 | 支气管狭窄因子(BCF)的半衰期 | h | 9.54 | 0.37 | - | 19.6 | 0.263 | - | |
| C50 | 生产50%的可回收呼气峰值流速(PEFR)时的茶碱浓度 | mg/L | 10.3 | 0.215 | - | 8.48 | 0.268 | - | |
| εtheo | 茶碱相对于支气管狭窄因子(BCF)效应的疗效 | - | 0.414 | 0.207 | - | 0.373 | 0.197 | - | |
| Hill exponent | 曲线陡度指数 | - | 3.25 | 0.25 | - | 2.59 | 0.3 | - | |
| IIV Base | - | 0.404 | 0.229 | 20.3 | 0.405 | 0.256 | 18.9 | ||
| IIV Normal | - | 0.389 | 0.221 | 16.6 | 0.164 | 0.364 | 43.4 | ||
| IIV T50 | - | 1.22 | 0.413 | 34 | 1.55 | 0.281 | 29.6 | ||
| IIV C50 | - | 0.68 | 0.638 | 48.6 | 0.664 | 0.609 | 48.2 | ||
| Proportional RUV | - | 0.145 | 0.14 | 30.4 | 0.159 | 0.123 | 25.8 | ||
| Diagnosis on Normal | 每个类别的典型值分数 | - | - | - | - | 0.202 | 0.174 | - | |
| Female on Normal | 女性的典型值分数 | - | - | - | - | -0.258 | 0.193 | - | |
| Years on Normal | 缩放因子 | - | - | - | - | -0.012 | 0.12 | - |
IIV和RUV值报告为对角线元素的标准偏差。 IIV和RUV的RSE，即NONMEM的方差-协方差矩阵估计值，以近似标准差标度报告（标准误差/方差估计值）/2。收缩值对应于标准差收缩。 PEFR：呼气峰值流速，BCF：支气管狭窄因子，RUV：残余的不明变异性，IIV：个体间变异，RSE：相对标准误差。 *使用SIR获得的RSE。 †对应于协变量模型具有以下特征的典型个体的值：男性，40岁，患有哮喘。
7.参考文献(中文翻译)
- Holford, N.; Hashimoto, Y.; Sheiner, L.B.时间和茶碱浓度有助于解释急性气道阻塞后峰值流量的恢复。Clinical pharmacokinetics 1993, 25, 506–515.
- Holford, N.; Black, P.; Couch, R.; Kennedy, J.; Briant, R.严重气道阻塞中的茶碱目标浓度 - 10 或 20 mg/l？Clinical pharmacokinetics 1993, 25, 495–505.
- Savic, R.M.; Karlsson, M.O.收缩在诊断经验贝叶斯估计中的重要性：问题和解决方案。The AAPS journal 2009, 11, 558–569.
- Lavielle, M.; Ribba, B.诊断定量药理学模型的增强方法：从条件分布中随机抽样。Pharmaceutical research 2016, 33, 2979–2988.
- Mandema, J.W.; Verotta, D.; Sheiner, L.B.建立群体药代动力学药效动力学模型。I. Models for Covariate Effects. Journal of pharmacokinetics and biopharmaceutics 1992, 20, 511–528.
- Jonsson, E.N.; Karlsson, M.O.Xpose–一种基于 s-PLUS 的 NONMEM 群体药代动力学/药效动力学模型构建辅助工具。Computer Methods and Programs in Biomedicine 1999, 58, 51–64, doi:10.1016/s0169-2607(98)00067-4.
- Keizer, R.J.; Karlsson, M.O.; Hooker, A.C.NONMEM 建模和仿真工作台：关于 Pirana、PsN 和 Xpose 的教程。CPT: Pharmacometrics & Systems Pharmacology 2013, 2, doi:10.1038/psp.2013.24.
- Kowalski, K.G.; Hutmacher, M.M.使用 Wald 似然比检验对群体模型中的协变量进行有效筛选。Journal of pharmacokinetics and pharmacodynamics 2001, 28, 253–275.
- Lindbom, L.; Ribbing, J.; Jonsson, E.N.Perl-speaks-NONMEM （PsN） — 用于 NONMEM 相关编程的 Perl 模块。Computer methods and programs in biomedicine 2004, 75, 85–94.
- Lindbom, L.; Pihlgren, P.; Jonsson, N.PsN-Toolkit — 使用 NONMEM 进行非线性混合效应建模的计算机密集型统计方法集合。Computer methods and programs in biomedicine 2005, 79, 241–257.
- Ribbing, J.; Nyberg, J.; Caster, O.; Jonsson, E.N.Lasso——一种在非线性混合效应模型中构建预测协变量模型的新方法。Journal of pharmacokinetics and pharmacodynamics 2007, 34, 485–517.
- Karlsson, M.O.基于参数和协变量协方差矩阵的全模型方法，PAGE 2012。
- Ivaturi, V.; Keizer, R.; Karlsson, M.O.表征协变量关系的全随机效应模型 WCOP 2012。
- Yun, H.; Niebecker, R.; Svensson, E.; Karlsson, M.O.FREM和FFEM的评估，包括模型线性化的使用，PAGE 2013。
- Hu, C.变异性和不确定性：定量药理学模拟和间隔的解释和使用。Journal of Pharmacokinetics and Pharmacodynamics 2022, 1–5.
- Jonsson, E.N.; Nyberg, J.在 Bootstrap 和视觉预测检验分析中选择百分位数估计样本数量的定量方法。CPT: Pharmacometrics & Systems Pharmacology 2022.
7 参考文献(英文原文)
- Holford, N.; Hashimoto, Y.; Sheiner, L.B. Time and Theophylline Concentration Help Explain the Recovery of Peak Flow Following Acute Airways Obstruction. Clinical pharmacokinetics 1993, 25, 506–515.
- Holford, N.; Black, P.; Couch, R.; Kennedy, J.; Briant, R. Theophylline Target Concentration in Severe Airways Obstruction—10 or 20 Mg/l? Clinical pharmacokinetics 1993, 25, 495–505.
- Savic, R.M.; Karlsson, M.O. Importance of Shrinkage in Empirical Bayes Estimates for Diagnostics: Problems and Solutions. The AAPS journal 2009, 11, 558–569.
- Lavielle, M.; Ribba, B. Enhanced Method for Diagnosing Pharmacometric Models: Random Sampling from Conditional Distributions. Pharmaceutical research 2016, 33, 2979–2988.
- Mandema, J.W.; Verotta, D.; Sheiner, L.B. Building Population Pharmacokineticpharmacodynamic Models. I. Models for Covariate Effects. Journal of pharmacokinetics and biopharmaceutics 1992, 20, 511–528.
- Jonsson, E.N.; Karlsson, M.O. Xpose–an s-PLUS Based Population Pharmacokinetic/Pharmacodynamic Model Building Aid for NONMEM. Computer Methods and Programs in Biomedicine 1999, 58, 51–64, doi:10.1016/s0169-2607(98)00067-4.
- Keizer, R.J.; Karlsson, M.O.; Hooker, A.C. Modeling and Simulation Workbench for NONMEM: Tutorial on Pirana, PsN, and Xpose. CPT: Pharmacometrics & Systems Pharmacology 2013, 2, doi:10.1038/psp.2013.24.
- Kowalski, K.G.; Hutmacher, M.M. Efficient Screening of Covariates in Population Models Using Wald’s Approximation to the Likelihood Ratio Test. Journal of pharmacokinetics and pharmacodynamics 2001, 28, 253–275.
- Lindbom, L.; Ribbing, J.; Jonsson, E.N. Perl-Speaks-NONMEM (PsN)—a Perl Module for NONMEM Related Programming. Computer methods and programs in biomedicine 2004, 75, 85–94.
- Lindbom, L.; Pihlgren, P.; Jonsson, N. PsN-Toolkit—a Collection of Computer Intensive Statistical Methods for Non-Linear Mixed Effect Modeling Using NONMEM. Computer methods and programs in biomedicine 2005, 79, 241–257.
- Ribbing, J.; Nyberg, J.; Caster, O.; Jonsson, E.N. The Lasso—a Novel Method for Predictive Covariate Model Building in Nonlinear Mixed Effects Models. Journal of pharmacokinetics and pharmacodynamics 2007, 34, 485–517.
- Karlsson, M.O. a Full Model Approach Based on the Covariance Matrix of Parameters and Covariates PAGE 2012.
- Ivaturi, V.; Keizer, R.; Karlsson, M.O. a Full Random Effects Model for Characterising Covariate Relations WCOP 2012.
- Yun, H.; Niebecker, R.; Svensson, E.; Karlsson, M.O. Evaluation of FREM and FFEM Including Use of Model Linearization PAGE 2013.
- Hu, C. Variability and Uncertainty: Interpretation and Usage of Pharmacometric Simulations and Intervals. Journal of Pharmacokinetics and Pharmacodynamics 2022, 1–5.
- Jonsson, E.N.; Nyberg, J. a Quantitative Approach to the Choice of Number of Samples for Percentile Estimation in Bootstrap and Visual Predictive Check Analyses. CPT: Pharmacometrics & Systems Pharmacology 2022.
8 附录
A NONMEM代码
A.1 出版物中的协变量模型(Covariate model from the publication) (run20)
;; 1. Based on: 11
$PROBLEM Covariate model from the publication
$DATA ../data/theo_no_missing.csv IGNORE=@
$INPUT ID TIME THEO AGE WT SEX RACE DIAG DV
$ESTIMATION METHOD=1 NOABORT MAXEVAL=9999 POSTHOC
$COVARIANCE
$THETA (0,141.587) ; TV_BASE (0,336.984) ; TV_NORMAL
(.01,7.27855) ; TV_T50
(.01,11.427) ; TV_C50
(0,0.463118,1) ; TV_ALPHA
(.1,2.82371,5) ; TV_HILL
0.01 ; DIAG
0.01 ; FEMALE
0.01 ; FYEARS
$OMEGA 0.160171 ; IIV_BASE 0.143395 ; IIV_NORMAL
1.7514 ; IIV_T50
0.487499 ; IIV_C50
$SIGMA 0.0193434 ; RUV_PROP
$PRED
; Group variables (FIXED effects) FDIAG = 1+THETA(7) * (1-DIAG) FSEX = 1+THETA(8) * (1-SEX) FAGE = 1+THETA(9) * (AGE-40)
TVNORMAL = THETA(2)
GRP_NORMAL = FDIAG*FAGE*FSEX*TVNORMAL
; Individual variables (RANDOM effects) TVBASE = THETA(1)
BASE = TVBASE*EXP(ETA(1)) NORMAL = GRP_NORMAL*EXP(ETA(2)) TVT50 = THETA(3)
T50 = TVT50*EXP(ETA(3))
TVC50 = THETA(4)
C50 = TVC50*EXP(ETA(4))
IF (T50.LE.0.01) EXIT 1 3
IF (C50.LE.0.01) EXIT 1 4
IF (TIME.LT.0) THEN LTZERO=1
ELSE
LTZERO=0
ENDIF
FTIME=LTZERO+(1-LTZERO)*EXP(-LOG(2)/T50*TIME) BCF=(NORMAL/BASE-1)*FTIME
FEMAX=BCF/(BCF+1) PEFRT=NORMAL*(1-FEMAX) HILL = THETA(6) CPN=THEO**HILL C50N=C50**HILL
PEFRCT=(NORMAL-PEFRT)*CPN/(CPN+C50N) ALPHA=THETA(5)
F = PEFRT + ALPHA * PEFRCT IPRED = F
IRES = DV - IPRED IWRES = IRES/IPRED
Y = F* ( 1 + EPS(1) )
$TABLE ID TIME THEO BASE NORMAL T50 C50 ALPHA HILL ETA1 ETA2 ETA3 ETA4 YONEHEADER NOPRINT FILE=run20.dat
$TABLE ID TIME YTHEO IPRED IWRES NOPRINT ONEHEADER
FILE=sdtab20
$TABLE ID TIME THEO BASE NORMAL T50 C50 ALPHA HILL ETA1 ETA2 ETA3 ETA4 NOPRINT ONEHEADER FILE=patab20
A.2 基础模型(Base model) (run11)
;; 1. Based on:
$PROBLEM Theophylline and time on PEFR
$DATA ../data/theo_no_missing.csv IGNORE=@
$INPUT ID TIME THEO AGE WT SEX RACE DIAG DV
$ESTIMATION METHOD=1 NOABORT MAXEVAL=9999 POSTHOC
$COVARIANCE
$THETA
(0,146.22) ; TV_BASE
(0,327.575) ; TV_NORMAL
(.01,6.06929) ; TV_T50
(.01,12.5879) ; TV_C50
(0,0.474818,1) ; TV_ALPHA
(.1,2.63332,5) ; TV_HILL
$OMEGA
0.164643 ; IIV_BASE
0.160737 ; IIV_NORMAL
1.59823 ; IIV_T50
0.41132 ; IIV_C50
$SIGMA 0.0190902 ; RUV_PROP
$PRED
; Individual variables (RANDOM effects) TVBASE = THETA(1)
BASE = TVBASE*EXP(ETA(1)) TVNORMAL = THETA(2)
NORMAL = TVNORMAL*EXP(ETA(2)) TVT50 = THETA(3)
T50 = TVT50*EXP(ETA(3))
TVC50 = THETA(4)
C50 = TVC50*EXP(ETA(4))
IF (T50.LE.0.01) EXIT 1 3
IF (C50.LE.0.01) EXIT 1 4
IF (TIME.LT.0) THEN LTZERO=1
ELSE
LTZERO=0
ENDIF
FTIME=LTZERO+(1-LTZERO)*EXP(-LOG(2)/T50*TIME) BCF=(NORMAL/BASE-1)*FTIME
FEMAX=BCF/(BCF+1) PEFRT=NORMAL*(1-FEMAX) HILL = THETA(6) CPN=THEO**HILL C50N=C50**HILL
PEFRCT=(NORMAL-PEFRT)*CPN/(CPN+C50N) ALPHA=THETA(5)
F = PEFRT + ALPHA * PEFRCT IPRED = F
IRES = DV - IPRED IWRES = IRES/IPRED
Y = F* ( 1 + EPS(1) )
$TABLE ID TIME THEO BASE NORMAL T50 C50 ALPHA HILL ETA1 ETA2 ETA3 ETA4 AGE WT SEX DIAG YONEHEADER NOPRINT FILE=run11.dat
$TABLE ID TIME YTHEO IPRED IWRES NOPRINT ONEHEADER FILE=sdtab11
$TABLE ID TIME THEO BASE NORMAL T50 C50 ALPHA HILL ETA1 ETA2 ETA3 ETA4 NOPRINT ONEHEADER FILE=patab11
$TABLE ID TIME AGE WT NOPRINT ONEHEADER FILE=cotab11
$TABLE ID TIME SEX DIAG YNOPRINT ONEHEADER FILE=catab11
A.3 FFEM (run22)
;; 1. Based on: 11
$PROBLEM FCM model
$DATA ../data/theo_no_missing.csv IGNORE=@
$INPUT ID TIME THEO AGE WT SEX RACE DIAG DV
$ESTIMATION METHOD=1 NOABORT MAXEVAL=9999 POSTHOC
$COVARIANCE
$THETA (0,146.22) ; TV_BASE (0,327.575) ; TV_NORMAL
(.01,6.06929) ; TV_T50
(.01,12.5879) ; TV_C50
(0,0.474818,1) ; TV_ALPHA
(.1,2.63332,5) ; TV_HILL
0.01 ; Diag on Base
0.01 ; Sex on Base
0.01 ; Age on Base
0.01 ; WT on Base
0.01 ; Diag on Normal
0.01 ; Sex on Normal
0.01 ; Age on Normal
0.01 ; WT on Normal
$OMEGA 0.164643 ; IIV_BASE 0.160737 ; IIV_NORMAL
1.59823 ; IIV_T50
0.41132 ; IIV_C50
$SIGMA 0.0190902 ; RUV_PROP
$PRED
; Group variables (FIXED effects) BDIAG = THETA(7) * (1-DIAG) BSEX = THETA(8) * (1-SEX) BAGE = THETA(9) * (AGE-40) BWT = THETA(10) * (WT-66) NDIAG = THETA(11) * (1-DIAG) NSEX = THETA(12) * (1-SEX) NAGE = THETA(13) * (AGE-40) NWT = THETA(14) * (WT-66)
; Individual variables (RANDOM effects)
COV_BASE = (1+BDIAG)*(1+BAGE)*(1+BSEX)*(1+BWT) TVBASE = THETA(1)*COV_BASE
BASE = TVBASE*EXP(ETA(1))
COV_NORMAL = (1+NDIAG)*(1+NAGE)*(1+NSEX)*(1+NWT) TVNORMAL = THETA(2)*COV_NORMAL
NORMAL = TVNORMAL*EXP(ETA(2)) TVT50 = THETA(3)
T50 = TVT50*EXP(ETA(3))
TVC50 = THETA(4)
C50 = TVC50*EXP(ETA(4))
IF (T50.LE.0.01) EXIT 1 3
IF (C50.LE.0.01) EXIT 1 4
IF (TIME.LT.0) THEN LTZERO=1
ELSE
LTZERO=0
ENDIF
FTIME=LTZERO+(1-LTZERO)*EXP(-LOG(2)/T50*TIME) BCF=(NORMAL/BASE-1)*FTIME
FEMAX=BCF/(BCF+1) PEFRT=NORMAL*(1-FEMAX) HILL = THETA(6) CPN=THEO**HILL C50N=C50**HILL
PEFRCT=(NORMAL-PEFRT)*CPN/(CPN+C50N) ALPHA=THETA(5)
F = PEFRT + ALPHA * PEFRCT IPRED = F
IRES = DV - IPRED IWRES = IRES/IPRED
Y = F* ( 1 + EPS(1) )
$TABLE ID TIME THEO BASE NORMAL T50 C50 ALPHA HILL ETA1 ETA2 ETA3 ETA4 AGE WT SEX DIAG YONEHEADER NOPRINT FILE=run22.dat
$TABLE ID TIME YTHEO IPRED IWRES NOPRINT ONEHEADER FILE=sdtab22
$TABLE ID TIME THEO BASE NORMAL T50 C50 ALPHA HILL ETA1 ETA2 ETA3 ETA4 NOPRINT ONEHEADER FILE=patab22
$TABLE ID TIME AGE WT NOPRINT ONEHEADER FILE=cotab22
$TABLE ID TIME SEX DIAG YNOPRINT ONEHEADER FILE=catab22
A.4 WAM (run24)
;; 1. Based on: 22
$PROBLEM Covariate model based on WAM
$DATA ../data/theo_no_missing.csv IGNORE=@
$INPUT ID TIME THEO AGE WT SEX RACE DIAG DV
$ESTIMATION METHOD=1 NOABORT MAXEVAL=9999 POSTHOC
$COVARIANCE
$THETA (0,164.582) ; TV_BASE (0,420.857) ; TV_NORMAL
(.01,12.3227) ; TV_T50
(.01,10.0245) ; TV_C50
(0,0.359849,1) ; TV_ALPHA
(.1,4.54423,5) ; TV_HILL
0 FIX ; Diag on Base
-0.169302 ; Sex on Base
-0.00533748 ; Age on Base
0 FIX ; WT on Base 0.210587 ; Diag on Normal
0 FIX ; Sex on Normal
-0.0111277 ; Age on Normal
0 FIX ; WT on Normal
$OMEGA 0.140716 ; IIV_BASE 0.0810301 ; IIV_NORMAL
1.06199 ; IIV_T50
0.318993 ; IIV_C50
$SIGMA 0.0233773 ; RUV_PROP
$PRED
; Group variables (FIXED effects) BDIAG = THETA(7) * (1-DIAG) BSEX = THETA(8) * (1-SEX) BAGE = THETA(9) * (AGE-40) BWT = THETA(10) * (WT-66) NDIAG = THETA(11) * (1-DIAG) NSEX = THETA(12) * (1-SEX) NAGE = THETA(13) * (AGE-40) NWT = THETA(14) * (WT-66)
; Individual variables (RANDOM effects)
COV_BASE = (1+BDIAG)*(1+BAGE)*(1+BSEX)*(1+BWT) TVBASE = THETA(1)*COV_BASE
BASE = TVBASE*EXP(ETA(1))
COV_NORMAL = (1+NDIAG)*(1+NAGE)*(1+NSEX)*(1+NWT) TVNORMAL = THETA(2)*COV_NORMAL
NORMAL = TVNORMAL*EXP(ETA(2)) TVT50 = THETA(3)
T50 = TVT50*EXP(ETA(3))
TVC50 = THETA(4)
C50 = TVC50*EXP(ETA(4))
IF (T50.LE.0.01) EXIT 1 3
IF (C50.LE.0.01) EXIT 1 4
IF (TIME.LT.0) THEN LTZERO=1
ELSE
LTZERO=0
ENDIF
FTIME=LTZERO+(1-LTZERO)*EXP(-LOG(2)/T50*TIME) BCF=(NORMAL/BASE-1)*FTIME
FEMAX=BCF/(BCF+1) PEFRT=NORMAL*(1-FEMAX) HILL = THETA(6) CPN=THEO**HILL C50N=C50**HILL
PEFRCT=(NORMAL-PEFRT)*CPN/(CPN+C50N) ALPHA=THETA(5)
F = PEFRT + ALPHA * PEFRCT IPRED = F
IRES = DV - IPRED IWRES = IRES/IPRED
Y = F* ( 1 + EPS(1) )
$TABLE ID TIME THEO BASE NORMAL T50 C50 ALPHA HILL ETA1 ETA2 ETA3 ETA4 AGE WT SEX DIAG YONEHEADER NOPRINT FILE=run24.dat
$TABLE ID TIME YTHEO IPRED IWRES NOPRINT ONEHEADER FILE=sdtab24
$TABLE ID TIME THEO BASE NORMAL T50 C50 ALPHA HILL ETA1 ETA2 ETA3 ETA4 NOPRINT ONEHEADER FILE=patab24
$TABLE ID TIME AGE WT NOPRINT ONEHEADER FILE=cotab24
$TABLE ID TIME SEX DIAG YNOPRINT ONEHEADER FILE=catab24
A.5 最终的LASSO模型(Final LASSO model) (run26)
;; 1. Based on: 11
$PROBLEM Covariate model based on LASSO
$DATA ../data/theo_no_missing.csv IGNORE=@
$INPUT ID TIME THEO AGE WT SEX RACE DIAG DV
$ESTIMATION METHOD=1 NOABORT MAXEVAL=9999 POSTHOC MSFO=psn_msf
$THETA (0,138.879) ; TV_BASE (0,333.281) ; TV_NORMAL
(.01,9.51597) ; TV_T50
(.01,11.7335) ; TV_C50
(0,0.535447,1) ; TV_ALPHA
(.1,1.94753,5) ; TV_HILL
$THETA -0.00270056670791727 FIX ; TH7 NORMALAGE
$THETA -0.397630255831705 FIX ; TH8 NORMALDIAG2
$THETA 0 FIX ; TH9 NORMALDIAG3
$THETA 0 FIX ; TH10 NORMALSEX1
$THETA 0 FIX ; TH11 NORMALWT
$THETA (-1000000,0.2) FIX ; TH12 T-VALUE
$OMEGA 0.158528 ; IIV_BASE 0.0615898 ; IIV_NORMAL
1.70203 ; IIV_T50
0.518568 ; IIV_C50
$SIGMA 0.0247062 ; RUV_PROP
$PRED
DIAG2 = 0
DIAG3 = 0
SEX1 = 0
IF (DIAG .EQ. 2) DIAG2=1 IF (DIAG .EQ. 3) DIAG3=1 IF (SEX .EQ. 1) SEX1=1
NORMALAGE = THETA(7)*(AGE-38.78030) NORMALDIAG2 = THETA(8)*(DIAG2-0.16667) NORMALDIAG3 = THETA(9)*(DIAG3-0.01515) NORMALSEX1 = THETA(10)*(SEX1-0.37879) NORMALWT = THETA(11)*(WT-67.22576)
NORMALCOV = (NORMALAGE+1)*(NORMALDIAG2+1)*(NORMALDIAG3+1)*(NORMALSEX1+1) NORMALCOV = NORMALCOV*(NORMALWT+1)
; Individual variables (RANDOM effects) TVBASE = THETA(1)
BASE = TVBASE*EXP(ETA(1)) TVNORMAL = THETA(2)
TVNORMAL = TVNORMAL*NORMALCOV NORMAL = TVNORMAL*EXP(ETA(2)) TVT50 = THETA(3)
T50 = TVT50*EXP(ETA(3))
TVC50 = THETA(4)
C50 = TVC50*EXP(ETA(4))
IF (T50.LE.0.01) EXIT 1 3
IF (C50.LE.0.01) EXIT 1 4
IF (TIME.LT.0) THEN LTZERO=1
ELSE
LTZERO=0
ENDIF
FTIME=LTZERO+(1-LTZERO)*EXP(-LOG(2)/T50*TIME) BCF=(NORMAL/BASE-1)*FTIME
FEMAX=BCF/(BCF+1) PEFRT=NORMAL*(1-FEMAX) HILL = THETA(6) CPN=THEO**HILL C50N=C50**HILL
PEFRCT=(NORMAL-PEFRT)*CPN/(CPN+C50N) ALPHA=THETA(5)
F = PEFRT + ALPHA * PEFRCT IPRED = F
IRES = DV - IPRED IWRES = IRES/IPRED
Y = F* ( 1 + EPS(1) )
$TABLE ID TIME THEO BASE NORMAL T50 C50 ALPHA HILL ETA1 ETA2 ETA3 ETA4 AGE WT SEX DIAG YONEHEADER NOPRINT FILE=run26.dat
$TABLE ID TIME YTHEO IPRED IWRES NOPRINT ONEHEADER FILE=sdtab26
$TABLE ID TIME THEO BASE NORMAL T50 C50 ALPHA HILL ETA1 ETA2 ETA3 ETA4 NOPRINT ONEHEADER FILE=patab26
$TABLE ID TIME AGE WT NOPRINT ONEHEADER FILE=cotab26
$TABLE ID TIME SEX DIAG YNOPRINT ONEHEADER FILE=catab26
A.6 最终的SCM模型(Final SCM model) (run25)
;; 1. Based on: 11
$PROBLEM Covariate model based on SCM
$DATA ../data/theo_no_missing.csv IGNORE=@
$INPUT ID TIME THEO AGE WT SEX RACE DIAG DV
$ESTIMATION METHOD=1 NOABORT MAXEVAL=9999 POSTHOC MCETA=1
$COVARIANCE
$THETA (0,146.71) ; TV_BASE (0,423.76) ; TV_NORMAL
(.01,42.4286) ; TV_T50
(.01,10.2693) ; TV_C50
(0,0.305535,1) ; TV_ALPHA
(.1,4.63383,5) ; TV_HILL
$THETA (-0.016,0.00557403,0.032) ; BASEWT1
$THETA (-0.024,0.0226863,0.051) ; C50AGE1
$THETA (-1,-0.496745,5) ; NORMALDIAG1 (-1,-0.2698,5) ; NORMALDIAG2
$THETA (-0.024,0.0442177,0.051) ; T50AGE1
$THETA (-1,-0.780861,5) ; T50SEX1
$THETA (-0.016,-0.0129475,0.032) ; T50WT1
$OMEGA 0.118039 ; IIV_BASE 0.0044012 ; IIV_NORMAL
2.8273 ; IIV_T50
0.328448 ; IIV_C50
$SIGMA 0.0249899 ; RUV_PROP
$PRED
;;; T50WT-DEFINITION START
T50WT = ( 1 + THETA(13)*(WT - 66))
;;; T50WT-DEFINITION END
;;; T50SEX-DEFINITION START IF(SEX.EQ.0) T50SEX = 1 ; Most common IF(SEX.EQ.1) T50SEX = ( 1 + THETA(12))
;;; T50SEX-DEFINITION END
;;; T50AGE-DEFINITION START
T50AGE = ( 1 + THETA(11)*(AGE - 34.5))
;;; T50AGE-DEFINITION END
;;; T50-RELATION START T50COV=T50AGE*T50SEX*T50WT
;;; T50-RELATION END
;;; NORMALDIAG-DEFINITION START IF(DIAG.EQ.1) NORMALDIAG = 1 ; Most common IF(DIAG.EQ.2) NORMALDIAG = ( 1 + THETA(9)) IF(DIAG.EQ.3) NORMALDIAG = ( 1 + THETA(10))
;;; NORMALDIAG-DEFINITION END
;;; NORMAL-RELATION START NORMALCOV=NORMALDIAG
;;; NORMAL-RELATION END
;;; C50AGE-DEFINITION START
C50AGE = ( 1 + THETA(8)*(AGE - 34.5))
;;; C50AGE-DEFINITION END
;;; C50-RELATION START C50COV=C50AGE
;;; C50-RELATION END
;;; BASEWT-DEFINITION START
BASEWT = ( 1 + THETA(7)*(WT - 66))
;;; BASEWT-DEFINITION END
;;; BASE-RELATION START BASECOV=BASEWT
;;; BASE-RELATION END
; Individual variables (RANDOM effects) TVBASE = THETA(1)
TVBASE = BASECOV*TVBASE
BASE = TVBASE*EXP(ETA(1)) TVNORMAL = THETA(2)
TVNORMAL = NORMALCOV*TVNORMAL
NORMAL = TVNORMAL*EXP(ETA(2)) TVT50 = THETA(3)
TVT50 = T50COV*TVT50
T50 = TVT50*EXP(ETA(3))
TVC50 = THETA(4)
TVC50 = C50COV*TVC50
C50 = TVC50*EXP(ETA(4))
IF (T50.LE.0.01) EXIT 1 3
IF (C50.LE.0.01) EXIT 1 4
IF (TIME.LT.0) THEN LTZERO=1
ELSE
LTZERO=0
ENDIF
FTIME=LTZERO+(1-LTZERO)*EXP(-LOG(2)/T50*TIME) BCF=(NORMAL/BASE-1)*FTIME
FEMAX=BCF/(BCF+1) PEFRT=NORMAL*(1-FEMAX) HILL = THETA(6) CPN=THEO**HILL C50N=C50**HILL
PEFRCT=(NORMAL-PEFRT)*CPN/(CPN+C50N) ALPHA=THETA(5)
F = PEFRT + ALPHA * PEFRCT IPRED = F
IRES = DV - IPRED IWRES = IRES/IPRED
Y = F* ( 1 + EPS(1) )
$TABLE ID TIME THEO BASE NORMAL T50 C50 ALPHA HILL ETA1 ETA2 ETA3 ETA4 AGE WT SEX DIAG YONEHEADER NOPRINT FILE=run25.dat
$TABLE ID TIME YTHEO IPRED IWRES NOPRINT ONEHEADER FILE=sdtab25
$TABLE ID TIME THEO BASE NORMAL T50 C50 ALPHA HILL ETA1 ETA2 ETA3 ETA4 NOPRINT ONEHEADER FILE=patab25
$TABLE ID TIME AGE WT NOPRINT ONEHEADER FILE=cotab25
$TABLE ID TIME SEX DIAG YNOPRINT ONEHEADER FILE=catab25
A.7 最终的FREM模型(Final FREM model) (run28)
;; 1. Based on: 27
$PROBLEM FREM final model (model 4)
$DATA frem_run11/frem_dataset.dta IGNORE=@
$INPUT ID TIME THEO AGE WT SEX RACE DIAG DV FREMTYPE
$ESTIMATION METHOD=1 NOABORT MAXEVAL=9999 POSTHOC NONINFETA=1 MCETA=1
$THETA (0,143.207) ; TV_BASE (0,331.877) ; TV_NORMAL
(.01,9.53588) ; TV_T50
(.01,10.303) ; TV_C50
(0,0.413845,1) ; TV_ALPHA
(.1,3.25128,5) ; TV_HILL
$THETA 67.2257575758 FIX ; TV_WT 38.7803030303 FIX ; TV_AGE
1.19696969697 FIX ; TV_DIAG
0.378787878788 FIX ; TV_SEX
$OMEGA BLOCK(8) 0.1632 ; IIV_BASE
0.00157182 0.151386 ; IIV_NORMAL
0.00491742 0.00473609 1.48168 ; IIV_T50
0.0027459 0.00264465 0.00827375 0.462009 ; IIV_C50
0.0323345 0.0123791 -0.153176 -0.0670133 1 ; BSV_WT
-0.0864764 -0.217291 0.443655 0.145727 0.177913 1 ; BSV_AGE
-0.0624184 -0.1921 0.24098 0.153299 -0.0255564 0.572045 1 ; BSV_DIAG
0.0729895 -0.0119927 -0.174831 -0.00915787 0.153527 0.225522 0.32921 1 ; BSV_SEX
$SIGMA 0.0209202 ; RUV_PROP
$SIGMA 0.0000001 FIX ; EPSCOV
$PRED
; INDIVIDUAL VARIABLES (RANDOM EFFECTS) TVBASE = THETA(1)
BASE = TVBASE*EXP(ETA(1)) TVNORMAL = THETA(2)
NORMAL = TVNORMAL*EXP(ETA(2)) TVT50 = THETA(3)
T50 = TVT50*EXP(ETA(3))
TVC50 = THETA(4)
C50 = TVC50*EXP(ETA(4))
IF (T50.LE.0.01) EXIT 1 3
IF (C50.LE.0.01) EXIT 1 4
IF (TIME.LT.0) THEN LTZERO=1
ELSE
LTZERO=0
ENDIF
FTIME=LTZERO+(1-LTZERO)*EXP(-LOG(2)/T50*TIME) BCF=(NORMAL/BASE-1)*FTIME
FEMAX=BCF/(BCF+1) PEFRT=NORMAL*(1-FEMAX) HILL = THETA(6) CPN=THEO**HILL C50N=C50**HILL
PEFRCT=(NORMAL-PEFRT)*CPN/(CPN+C50N) ALPHA=THETA(5)
F = PEFRT + ALPHA * PEFRCT IPRED = F
IRES = DV - IPRED IWRES = IRES/IPRED
Y = F* ( 1 + EPS(1) )
;;;FREM CODE BEGIN COMPACT
;;;DO NOT MODIFY
SDC5 = 14.7155140713
SDC6 = 18.976206232
SDC7 = 0.43579170631
SDC8 = 0.486933119697
IF (FREMTYPE.EQ.100) THEN
; WT 14.7155140713
Y = THETA(7) + ETA(5)*SDC5 + EPS(2) IPRED = THETA(7) + ETA(5)*SDC5
END IF
IF (FREMTYPE.EQ.200) THEN
; AGE 18.976206232
Y = THETA(8) + ETA(6)*SDC6 + EPS(2) IPRED = THETA(8) + ETA(6)*SDC6
END IF
IF (FREMTYPE.EQ.300) THEN
; DIAG 0.43579170631
Y = THETA(9) + ETA(7)*SDC7 + EPS(2) IPRED = THETA(9) + ETA(7)*SDC7
END IF
IF (FREMTYPE.EQ.400) THEN
; SEX 0.486933119697
Y = THETA(10) + ETA(8)*SDC8 + EPS(2) IPRED = THETA(10) + ETA(8)*SDC8
END IF
;;;FREM CODE END COMPACT
$COVARIANCE UNCONDITIONAL PRECOND=1
$TABLE ID TIME THEO BASE NORMAL T50 C50 ALPHA HILL ETA1 ETA2 ETA3 ETA4 AGE WT SEX DIAG YNOTITLE ONEHEADER NOPRINT
FILE=run28.dat
$TABLE ID TIME YTHEO IPRED IWRES NOPRINT NOTITLE ONEHEADER
FILE=sdtab28
$TABLE ID TIME THEO BASE NORMAL T50 C50 ALPHA HILL ETA1 ETA2 ETA3 ETA4 NOPRINT NOTITLE ONEHEADER FILE=patab28
$TABLE ID TIME AGE WT NOPRINT NOTITLE ONEHEADER FILE=cotab28
$TABLE ID TIME SEX DIAG YNOPRINT NOTITLE ONEHEADER FILE=catab28
$ETAS FILE=frem_run11/final_models/model_4_input.phi
B R代码
B.1 数据管理(Data management)
用于数据管理的 R 代码。
dm <- fread("data/theo_no_missing.csv") # 1. Import data
dm <- subset( dm, select = -c(RACE)) # 2. RACE removed from the analysis
dm$SEX <- as.factor(as.character( dm$SEX)) # 3. Convert numerics to factors
dm$DIAG <- as.factor(as.character( dm$DIAG))
dm$PEFR <- as.numeric( dm$PEFR) # 4. Set numbers to numerics
B.2 数值摘要(Numerical summary)
dm_tab <- dm %>%
mutate( # Rename factors
Diagnosis = ifelse( DIAG == 1, "1: Asthma",
ifelse( DIAG == 2, "2: COPD", "3: COPD and asthma")
),
Sex = ifelse( SEX == 0, "0: Female", "1: Male"),
`Age (years)` = AGE, # Rename variables
`Theophylline concentrations (mg/L)` = THEO,
`Peak expiratory force rate (PEFR, L/min)` = PEFR,
`Weight (kg)` = WT
)
dp <- data.frame(dm_tab %>% # Extract dependent variables
select(`Theophylline concentrations (mg/L)`,
`Peak expiratory force rate (PEFR, L/min)`) %>%
tbl_summary() %>%
as_gt())
cov <- data.frame( dm_tab %>% # Extract covariates
distinct(ID, .keep_all = TRUE) %>% # Keep 1 row per ID
select(`Age (years)`, `Weight (kg)`, Sex, Diagnosis) %>%
tbl_summary(digits = list(
c('Age (years)', 'Weight (kg)', Sex, Diagnosis) ~ c(1))) %>%
as_gt())
rb <- rbind(dp, cov) %>% # Merge covariates and dependent variable summary
filter(stat_0 != "") %>% # Filter
mutate(label = ifelse(row_type %in% c("label"), " ", label))
rb %>% # Create table
select(variable, label, stat_0) %>%
dplyr::rename("Metrics*" = stat_0,
"Categories" = label,
"Variables" = variable) %>%
kable(booktabs = T,
caption = "Numerical description of the Theophylline data set") %>%
collapse_rows(columns = 1,
latex_hline = "none",
valign = "top") %>%
kable_styling(latex_options = "H") %>%
pack_rows("Dependent variables (526 observations)", 1, 2) %>%
pack_rows("Continuous covariates (132 subjects)", 3, 4, hline_before = T) %>%
pack_rows("Categorical covariates (132 subjects)", 5, 9, hline_before = T) %>%
kableExtra::footnote(
symbol = "Median (inter-quartile range) for continuous variables; n(%) for categorical variables.",
symbol_title = "")
B.3 茶碱数据文件详情(Theophylline data file details)
表 S9：茶碱数据文件的描述。
| 列 | 描述 | 单位 | 值 |
|---|---|---|---|
| ID | 受试者唯一标识符 | - | 整数> 0 |
| TIME | 时间 | hours | 数值> 0 |
| THEO | 茶碱血清浓度 | mg/mL | 数值> 0 |
| AGE | 年龄 | years | 整数> 1 |
| WT | 体重 | kg | 数值> 1 |
| SEX | 性别 | - | 0: 女性, 1: 男性 |
| DIAG | 诊断(分类尺度) | - | 1:哮喘,2:COPD,3:COPD和哮喘 |
| PEFR | 呼气峰值流速 | L/min | 数值> 0 |
COPD: 慢性阻塞性肺病(chronic obstructive pulmonary disease)
表 S10：茶碱数据文件的前 10 行。
| ID | TIME | THEO | AGE | WT | SEX | DIAG | PEFR |
|---|---|---|---|---|---|---|---|
| 1 | 0.01 | 1 | 27 | 57 | 0 | 1 | 200 |
| 1 | 1.51 | 20.7 | 27 | 57 | 0 | 1 | 300 |
| 2 | 0.01 | 0.1 | 21 | 76 | 0 | 1 | 110 |
| 2 | 1.42 | 25.5 | 21 | 76 | 0 | 1 | 200 |
| 2 | 4.42 | 26.2 | 21 | 76 | 0 | 1 | 325 |
| 3 | 0.01 | 0.1 | 26 | 67.5 | 1 | 1 | 150 |
B.4 意大利面条图(Spaghettis plots)
ggplot(dm, aes(y = PEFR, x= THEO)) +
geom_point(aes(group = ID)) +
geom_line(aes(group = ID)) +
geom_smooth(se = FALSE, color = "red") +
xlab("Observed theophylline concentrations (mg/mL)") + ylab("Observed PEFR (L/min)")+
theme(legend.position = "none") +
theme_bw()
B.5 散点图矩阵(Scatter plot matrix)
dmn <- dm %>%
mutate( # Rename factors
Diagnosis = ifelse( DIAG == 1, "Asthma",
ifelse( DIAG == 2, "COPD", "COPD and asthma")),
Sex = ifelse( SEX == 0, "Female", "Male"),
Weight = WT, # Rename covariates
Age = AGE
)
cov <- dmn[, c("Age", "Weight", "Sex", "Diagnosis")] # Select covariates columns
ggpairs(cov,
upper = list(continuous = "cor", combo = "box_no_facet"),
lower = list(continuous = "smooth", combo = "dot_no_facet")) +
theme_bw() +
theme(axis.text.x = element_text( angle=45, hjust=1 ) )
B.6 拟合优度图(Goodness-of-fit plots)
B.7 协变量对经验贝叶斯估计值图(Covariates vs EBEs)
#Loading the data
input <- fread("models/run11.dat") # NM output table
### Data management
input <- input[!duplicated(input$ID) , ] # Keep one line per ID
names(input)[names(input) == "AGE"] <- "Age" #Rename interesting columns
names(input)[names(input) == "WT"] <- "Weight"
names(input)[names(input) == "SEX"] <- "Sex"
names(input)[names(input) == "DIAG"] <- "Diagnosis"
ebes <- # Keep only relevant columns
input[, c("ID", "ETA1", "ETA2", "ETA3", "ETA4", "Age", "Weight", "Sex", "Diagnosis")]
ebes <- melt( # Get long format
ebes,
id = c("ID", "Age", "Weight", "Sex", "Diagnosis"), variable.name = "ETA",
value.name = "EBEs"
)
ebes <- melt( # Get long format
ebes,
id = c("ID", "EBEs", "ETA"),
variable.name = "COV", value.name = "Covariates"
)
# Change name for plot
ebes$ETA <- as.character(ebes$ETA)
ebes$ETA[ ebes$ETA %in% c("ETA1") ] <- "Base"
ebes$ETA[ ebes$ETA %in% c("ETA2") ] <- "Normal"
ebes$ETA[ ebes$ETA %in% c("ETA3") ] <- "T50"
ebes$ETA[ ebes$ETA %in% c("ETA4") ] <- "C50"
ebes$ETA <- as.factor(ebes$ETA)
levels(ebes$ETA) <- levels(ebes$ETA)[c(1,3,2,4)]
sum <- xpose::get_summary(xpdb11) # Get etas values
etas <- sum$value[sum$descr %in% c("Eta shrinkage")]
etas <- as.numeric(gsub(" .*", "", unlist(strsplit(etas, "], "))))
# Add the shrinkage information
ebes$Shrinkage <- NA
ebes$Shrinkage[ebes$ETA %in% c("Base")] <- paste0("S(SD)=", etas[1],"%")
ebes$Shrinkage[ebes$ETA %in% c("Normal")] <- paste0("S(SD)=", etas[2],"%")
ebes$Shrinkage[ebes$ETA %in% c("T50")] <- paste0("S(SD)=", etas[3],"%")
ebes$Shrinkage[ebes$ETA %in% c("C50")] <- paste0("S(SD)=", etas[4],"%")
# Divide into continuous and categorical cov
cont <- ebes[ ebes$COV %in% c("Age", "Weight"),]
cat <- ebes[!ebes$COV %in% c("Age", "Weight"), ]
# Create and rename factors
cat$Covariates[ cat$COV %in% c("Sex") & cat$Covariates == 0 ] <- "Female"
cat$Covariates[ cat$COV %in% c("Sex") & cat$Covariates == 1 ] <- "Male"
cat$Covariates[ cat$COV %in% c("Diagnosis") & cat$Covariates == 1 ] <- "Asthma"
cat$Covariates[ cat$COV %in% c("Diagnosis") & cat$Covariates == 2 ] <- "COPD"
cat$Covariates[ cat$COV %in% c("Diagnosis") & cat$Covariates == 3 ] <- "COPD and asthma"
cat$Covariates <- as.factor(cat$Covariates)
# Plot
contp <- ggplot(cont, aes(y = EBEs, x = Covariates)) + geom_point() +
facet_grid(ETA ~ COV, scales = "free") + geom_smooth(method = "lm",
colour = "red", se = FALSE) +
xlab("Continuous covariates") + theme_bw() +
theme( strip.background.y = element_blank(), strip.text.y = element_blank())
catp <- ggplot(cat, aes(y = EBEs, x = Covariates)) + geom_boxplot() +
facet_grid(ETA + Shrinkage ~ COV, scales = "free") + xlab("Categorical covariates") +
ylab(NULL) +
theme_bw() +
theme(axis.text.x = element_text(angle = 35, vjust = 1, hjust = 1))
plot1 <- plot_grid(contp, catp, nrow = 1, align = "h")
B.8 协变量对η抽样值图(Covariates vs η samples)
#Loading the data
input <- fread("models/run11.dat") # NM output table
phi <- fread( "models/run11.phi" ) # phi file
### Data management
input <- input[!duplicated(input$ID) , ] # Keep one line per ID
names(input)[names(input) == "AGE"] <- "Age" #Rename interesting columns
names(input)[names(input) == "WT"] <- "Weight"
names(input)[names(input) == "SEX"] <- "Sex"
names(input)[names(input) == "DIAG"] <- "Diagnosis"
names(phi) <- gsub("[()]|,", "", names(phi)) # Remove parenthesis and coma from header
# Get eta samples from the individual distributions of the phi file
fun <- function(v1, v2) { val <- rnorm(1,v1,v2) return(val)
}
phi <- phi %>%
mutate( ETAS1 = purrr::pmap_dbl(list( ETA1, ETC11), fun ),
ETAS2 = purrr::pmap_dbl(list( ETA2, ETC22), fun ),
ETAS3 = purrr::pmap_dbl(list( ETA3, ETC33), fun ),
ETAS4 = purrr::pmap_dbl(list( ETA4, ETC44), fun ) )
phi <- merge( input, phi[,c(2,18:21)] ) # Merge etas samples and covariates
etas <- # Keep only relevant columns
phi[, c("ID", "ETAS1", "ETAS2", "ETAS3", "ETAS4", "Age", "Weight", "Sex", "Diagnosis")]
etas <- melt( # Get long format: stack ETAS
etas,
id = c("ID", "Age", "Weight", "Sex", "Diagnosis"), variable.name = "ETAS",
value.name = "Samples"
)
etas <- melt( # Get long format: stack covariates
etas,
id = c("ID", "ETAS", "Samples"), variable.name = "COV", value.name = "Covariates"
)
# Change name for plot
etas$ETAS <- as.character(etas$ETAS)
etas$ETAS[ etas$ETAS %in% c("ETAS1") ] <- "Base"
etas$ETAS[ etas$ETAS %in% c("ETAS2") ] <- "Normal"
etas$ETAS[ etas$ETAS %in% c("ETAS3") ] <- "T50"
etas$ETAS[ etas$ETAS %in% c("ETAS4") ] <- "C50"
etas$ETAS <- as.factor(etas$ETAS) levels(etas$ETAS) <- levels(etas$ETAS)[c(1,3,2,4)]
sum <- xpose::get_summary(xpdb11) # Get etas values
eta_s <- sum$value[sum$descr %in% c("Eta shrinkage")]
eta_s <- as.numeric(gsub(" .*", "", unlist(strsplit(eta_s, "], "))))
# Add the shrinkage information
etas$Shrinkage <- NA
etas$Shrinkage[etas$ETAS %in% c("Base")] <- paste0("S(SD)=", eta_s[1],"%")
etas$Shrinkage[etas$ETAS %in% c("Normal")] <- paste0("S(SD)=", eta_s[2],"%")
etas$Shrinkage[etas$ETAS %in% c("T50")] <- paste0("S(SD)=", eta_s[3],"%")
etas$Shrinkage[etas$ETAS %in% c("C50")] <- paste0("S(SD)=", eta_s[4],"%")
# Divide into continuous and categorical cov
conts <- etas[ etas$COV %in% c("Age", "Weight"),]
cats <- etas[ etas$COV %in% c("Sex", "Diagnosis"), ]
# Create and rename factors
cats$Covariates[ cats$COV %in% c("Sex") & cats$Covariates == 0 ] <- "Female"
cats$Covariates[ cats$COV %in% c("Sex") & cats$Covariates == 1 ] <- "Male"
cats$Covariates[ cats$COV %in% c("Diagnosis") & cats$Covariates == 1 ] <- "Asthma"
cats$Covariates[ cats$COV %in% c("Diagnosis") & cats$Covariates == 2 ] <- "COPD"
cats$Covariates[ cats$COV %in% c("Diagnosis") & cats$Covariates == 3 ] <- "COPD and asthma"
cats$Covariates <- as.factor(cats$Covariates)
# Plot
contps <- ggplot(conts, aes(y = Samples, x = Covariates)) + geom_point() +
facet_grid(ETAS ~ COV, scales = "free") + geom_smooth(method = "lm",
colour = "red", se = FALSE) +
xlab("Continuous covariates") + ylab("Eta samples") + theme_bw() +
theme( strip.background.y = element_blank(), strip.text.y = element_blank())
catps <- ggplot(cats, aes(y = Samples, x= Covariates)) +
geom_boxplot() +
facet_grid(ETAS + Shrinkage ~ COV, scales = "free") + xlab("Categorical covariates") +
ylab(NULL) + theme_bw() +
theme(axis.text.x = element_text(angle = 35, vjust = 1, hjust = 1))
plot2 <- plot_grid(contps, catps, nrow = 1, align = "h")
B.9 GAM图
aic_plot <- xpose4::xp.akaike.plot(gamobj = xpgam) # akaike plot
res_plot <- xpose4::xp.plot(gamobj = xpgam) # Residuals plot
B.10 WAM
• 用于计算FFEM所有协变量子模型的LRT统计量Wald 近似值的函数。
wam <- function(k, # no. of covariate thetas in FFEM
p, # no. of parameters in theta, omega and sigma in full model
n, # no. of observations in data set
theta, # Final fixed covariate effect estimates
cov # Fixed covariate effect estimates var-covar error matrix
) {
# Create a matrix with all possible covariates prm combinations
kk <- 2 ˆ ((k - 1):0)
maker <-
paste("rep(rep(c(0,1),rep(" , kk , ",2))," , rev(kk) , ")" , sep = "") x<- apply(matrix(maker), 1, function(x)
eval(parse(text = x)))
kkk <- dim(x)[1] # Nb of columns in the matrix = fixed cov effect
# i= 1
ireg <- rep(1, k) idel <- 1:k
c2 <- cov[idel, idel] theta2 <- t(theta[idel])
lrt <- t(theta2) %*% solve(c2) %*% theta2 s <- p - length(idel)
sbc <- -0.5 * (lrt + s* log(n)) results <- data.frame(
i = 1:kkk,
ireg = rep(0, kkk), lrt = rep(0, kkk), sbc = rep(0, kkk)
)
results[1, 2:4] <- c(paste(ireg, collapse = ","), lrt, sbc)
for (i in 2:(kkk - 1))
{
ireg <- (1:k)[x[i, ] > 0]
idel <- (1:k)[x[i, ] == 0] c2 <- cov[idel, idel] theta2 <- t(theta[idel])
lrt <- t(theta2) %*% solve(c2) %*% theta2 s <- p - length(idel)
sbc <- -0.5 * (lrt + s* log(n))
results[i, 2:4] <- c(paste(ireg, collapse = ","), lrt, sbc)
}
# i= kkk ireg <- (1:k) lrt <- 0
sbc <- -0.5 * (lrt + p* log(n))
results[kkk, 2:4] <- c(paste(ireg, collapse = ","), lrt, sbc) results <- results[order(-as.numeric(results$sbc)), ] results[, "i"] <- 1:kkk
results
}
• 提取固定效应协变量参数的方差-协方差误差矩阵和FFEM的最终效应估计。
# Information from the FFEM
ntheta <- 14 # no. of thetas in FFEM
ncovtheta <- 8 # no. of covariate thetas in FFEM
run.no <- 22 # your run number
# Get the variance-covariance error matrix for fixed covariates effects
tc <- # Import NONMEM .cov file of FFEM
read.table( # .cov file = full variance-covariance error matrix of thetas, sigmas and omegas
file = paste("models/run", run.no, ".cov", sep = ""), skip = 1,
header = 1,
row.names = 1
)
fthetas <- ntheta - ncovtheta # Nb of thetas that are not covariate effects
tcnames <- names(tc)[(tc != 0)[1, ]][(fthetas+1):ntheta] # Names of that thetas
tc <- matrix( # Var cov matrix with only estimated parameters
tc[tc != 0], ncol = sqrt(length(tc[tc != 0]))
)
cov <- # Subset fixed covariates effects and add names
tc[(fthetas+1):ntheta, (fthetas+1):ntheta] cov[col(cov) > row(cov)] <- 0
cov <- cov + t(cov) - unlist(diag(unlist((diag(cov))))) dimnames(cov) <- list(theta = tcnames,
theta = tcnames)
# Get final estimates for fixed covariates effects
tp <- read.table( # Import NONMEM .ext file of FFEM
# Raw output file with numerical NONMEM results
file = paste("models/run", run.no, ".ext", sep = ""), skip = 1,
header = 1
)
tp <- # .ext line with final estimates and OFV
tp[tp$ITERATION == -1000000000, ]
tp <- tp[, tp != 0] # Only estimated parameters
theta <- tp[(1 + fthetas + 1):(1 + ntheta)] # Only fixed covariates effects thetas <- unlist(strsplit(names(theta), "THETA")) # Keep only the theta number thetas <- thetas[thetas != ""]
• 对来自 FFEM 的信息运行 WAM 算法。
results <- wam( # Run the WAM method on the FFEM (run22)
k = ncovtheta, # no. of covariate thetas in FFEM
p = 19, # no. of parameters in theta, omega and sigma in full model
n = 526, # no. of observations in data set
theta = theta, # Final fixed covariate effect estimates
cov = cov # Fixed covariate effect estimates var-covar error matrix
)
B.11 SCM
B.11.1 SCM的目标函数值下降图(OFV drop plot for SCM)
scm.short.log <- 'models/scm_run14/short_scmlog.txt'
list_incl_cov <- included_covariates(scm.short.log) n1 <-
list_incl_cov$n1 #Number of covariate included after forward step
sign <- list_incl_cov$sign data <- list_incl_cov$data name <- list_incl_cov$name
# plot SCM results included covariates
p <- plot_included_covariates(data, sign, n1, name) + theme_bw() +
ggtitle(NULL) +
theme(axis.text.x = element_text(angle = 45, hjust=1)) print(p)
B.11.2 SCM输出的文本摘要(SCM text summary output)
## Model directory /green/home/USER/estch718/isop_covariates/models/scm_run14/m1
##
## MODEL TEST BASE OFV NEW OFV TEST OFV (DROP) GOAL dDF SIGNIFICANT PVAL
## BASEAGE-2 PVAL 4962.29196 4952.05523 10.23673 > 3.84150 1 YES! 0.001377
## BASEDIAG-2 PVAL 4962.29196 4954.45130 7.84066 > 5.99150 2 YES! 0.019835
## BASESEX-2 PVAL 4962.29196 4955.05010 7.24186 > 3.84150 1 YES! 0.007122
## BASEWT-2 PVAL 4962.29196 4957.62887 4.66308 > 3.84150 1 YES! 0.030818
## C50AGE-2 PVAL 4962.29196 4898.86897 63.42299 > 3.84150 1 YES! 1.67e-15
## C50DIAG-2 PVAL 4962.29196 4937.24279 25.04916 > 5.99150 2 YES! 0.000004
## C50SEX-2 PVAL 4962.29196 4959.22473 3.06723 > 3.84150 1 0.079886
## C50WT-2 PVAL 4962.29196 4959.05895 3.23301 > 3.84150 1 0.072168
## NORMALAGE-2 PVAL 4962.29196 4904.83901 57.45295 > 3.84150 1 YES! 3.46e-14
## NORMALDIAG-2 PVAL 4962.29196 4883.73491 78.55705 > 5.99150 2 YES! 8.74e-18
## NORMALSEX-2 PVAL 4962.29196 4962.13938 0.15257 > 3.84150 1 0.696090
## NORMALWT-2 PVAL 4962.29196 4958.22705 4.06491 > 3.84150 1 YES! 0.043783
## T50AGE-2 PVAL 4962.29196 4932.99364 29.29832 > 3.84150 1 YES! 6.20e-08
## T50DIAG-2 PVAL 4962.29196 4927.98398 34.30798 > 5.99150 2 YES! 3.55e-08
## T50SEX-2 PVAL 4962.29196 4958.15679 4.13516 > 3.84150 1 YES! 0.042001
## T50WT-2 PVAL 4962.29196 4956.29366 5.99829 > 3.84150 1 YES! 0.014320
##
## Parameter-covariate relation chosen in this forward step: NORMAL-DIAG-2
## CRITERION PVAL < 0.05
## BASE_MODEL_OFV 4962.29196
## CHOSEN_MODEL_OFV 4883.73491
## Relations included after this step:
## BASE
## C50
## NORMAL DIAG-2
## T50
## --------------------
##
## Model directory /green/home/USER/estch718/isop_covariates/models/scm_run14/forward_scm_dir1/m1
##
## MODEL TEST BASE OFV NEW OFV TEST OFV (DROP) GOAL dDF SIGNIFICANT PVAL
## BASEAGE-2 PVAL 4883.73491 4877.07097 6.66394 > 3.84150 1 YES! 0.009838
## BASEDIAG-2 PVAL 4883.73491 4871.76993 11.96498 > 5.99150 2 YES! 0.002523
## BASESEX-2 PVAL 4883.73491 4872.96706 10.76786 > 3.84150 1 YES! 0.001033
## BASEWT-2 PVAL 4883.73491 4879.35381 4.38110 > 3.84150 1 YES! 0.036340
## C50AGE-2 PVAL 4883.73491 4845.35599 38.37893 > 3.84150 1 YES! 5.83e-10
## C50DIAG-2 PVAL 4883.73491 4881.28372 2.45119 > 5.99150 2 0.293580
## C50SEX-2 PVAL 4883.73491 4880.80471 2.93020 > 3.84150 1 0.086937
## C50WT-2 PVAL 4883.73491 4881.35728 2.37763 > 3.84150 1 0.123080
## NORMALAGE-2 PVAL 4883.73491 4870.69693 13.03798 > 3.84150 1 YES! 0.000305
## NORMALSEX-2 PVAL 4883.73491 4866.78023 16.95468 > 3.84150 1 YES! 0.000038
## NORMALWT-2 PVAL 4883.73491 4878.51777 5.21714 > 3.84150 1 YES! 0.022365
## T50AGE-2 PVAL 4883.73491 4860.40668 23.32823 > 3.84150 1 YES! 0.000001
## T50DIAG-2 PVAL 4883.73491 4881.29294 2.44197 > 5.99150 2 0.294940
## T50SEX-2 PVAL 4883.73491 4866.27328 17.46164 > 3.84150 1 YES! 0.000029
## T50WT-2 PVAL 4883.73491 4879.11279 4.62212 > 3.84150 1 YES! 0.031562
##
## Parameter-covariate relation chosen in this forward step: C50-AGE-2
## CRITERION PVAL < 0.05
## BASE_MODEL_OFV 4883.73491
## CHOSEN_MODEL_OFV 4845.35599
## Relations included after this step:
## BASE
## C50 AGE-2
## NORMAL DIAG-2
## T50
## --------------------
##
## Model directory /green/home/USER/estch718/isop_covariates/models/scm_run14/forward_scm_dir1/scm_dir1/m1
##
## MODEL TEST BASE OFV NEW OFV TEST OFV (DROP) GOAL dDF SIGNIFICANT PVAL
## BASEAGE-2 PVAL 4845.35599 4848.65200 -3.29602 > 3.84150 1 9999
## BASEDIAG-2 PVAL 4845.35599 4850.96014 -5.60415 > 5.99150 2 9999
## BASESEX-2 PVAL 4845.35599 4840.26182 5.09417 > 3.84150 1 YES! 0.024006
## BASEWT-2 PVAL 4845.35599 4843.55534 1.80065 > 3.84150 1 0.179630
## C50AGE-3 PVAL 4845.35599 4848.54735 -3.19137 > 3.84150 1 9999
## C50DIAG-2 PVAL 4845.35599 4848.62926 -3.27327 > 5.99150 2 9999
## C50SEX-2 PVAL 4845.35599 4850.38852 -5.03253 > 3.84150 1 9999
## C50WT-2 PVAL 4845.35599 4846.56889 -1.21291 > 3.84150 1 9999
## NORMALAGE-2 PVAL 4845.35599 4840.72917 4.62682 > 3.84150 1 YES! 0.031476
## NORMALSEX-2 PVAL 4845.35599 4838.39465 6.96134 > 3.84150 1 YES! 0.008329
## NORMALWT-2 PVAL 4845.35599 4850.53065 -5.17467 > 3.84150 1 9999
## T50AGE-2 PVAL 4845.35599 4841.77384 3.58215 > 3.84150 1 0.058404
## T50DIAG-2 PVAL 4845.35599 4846.75786 -1.40187 > 5.99150 2 9999
## T50SEX-2 PVAL 4845.35599 4836.68161 8.67438 > 3.84150 1 YES! 0.003227
9999
## Parameter-covariate relation chosen in this forward step: T50-SEX-2
## CRITERION PVAL < 0.05
## BASE_MODEL_OFV 4845.35599
## CHOSEN_MODEL_OFV 4836.68161
## Relations included after this step:
## BASE
## C50 AGE-2
## NORMAL DIAG-2
## T50 SEX-2
## --------------------
##
## Model directory /green/home/USER/estch718/isop_covariates/models/scm_run14/forward_scm_dir1/scm_dir1/scm_dir1/m1
##
## MODEL TEST BASE OFV NEW OFV TEST OFV (DROP) GOAL dDF SIGNIFICANT PVAL
## BASEAGE-2 PVAL 4836.68161 4825.92119 10.76042 > 3.84150 1 YES! 0.001037
## BASEDIAG-2 PVAL 4836.68161 4836.10614 0.57547 > 5.99150 2 0.749960
## BASESEX-2 PVAL 4836.68161 4822.16658 14.51502 > 3.84150 1 YES! 0.000139
## BASEWT-2 PVAL 4836.68161 4826.67158 10.01003 > 3.84150 1 YES! 0.001557
## C50AGE-3 PVAL 4836.68161 4841.00847 -4.32687 > 3.84150 1 9999
## C50DIAG-2 PVAL 4836.68161 4832.32558 4.35602 > 5.99150 2 0.113270
## C50SEX-2 PVAL 4836.68161 4832.13665 4.54496 > 3.84150 1 YES! 0.033016
## C50WT-2 PVAL 4836.68161 4830.37802 6.30359 > 3.84150 1 YES! 0.012049
## NORMALAGE-2 PVAL 4836.68161 4821.43645 15.24515 > 3.84150 1 YES! 0.000094
## NORMALSEX-2 PVAL 4836.68161 4836.79028 -0.10867 > 3.84150 1 9999
## NORMALWT-2 PVAL 4836.68161 4830.99661 5.68499 > 3.84150 1 YES! 0.017111
## T50AGE-2 PVAL 4836.68161 4817.49657 19.18504 > 3.84150 1 YES! 0.000012
## T50DIAG-2 PVAL 4836.68161 4832.57805 4.10355 > 5.99150 2 0.128510
## T50WT-2 PVAL 4836.68161 4832.42314 4.25847 > 3.84150 1 YES! 0.039055
##
## Parameter-covariate relation chosen in this forward step: T50-AGE-2
## CRITERION PVAL < 0.05
## BASE_MODEL_OFV 4836.68161
## CHOSEN_MODEL_OFV 4817.49657
## Relations included after this step:
## BASE
## C50 AGE-2
## NORMAL DIAG-2
## T50 AGE-2 SEX-2
## --------------------
##
## Model directory /green/home/USER/estch718/isop_covariates/models/scm_run14/forward_scm_dir1/scm_dir1/scm_dir1/scm_dir1/m1
##
## MODEL TEST BASE OFV NEW OFV TEST OFV (DROP) GOAL dDF SIGNIFICANT PVAL
## BASEAGE-2 PVAL 4817.49657 4812.03460 5.46197 > 3.84150 1 YES! 0.019435
## BASEDIAG-2 PVAL 4817.49657 4812.56759 4.92898 > 5.99150 2 0.085052
## BASESEX-2 PVAL 4817.49657 4808.11111 9.38545 > 3.84150 1 YES! 0.002187
## BASEWT-2 PVAL 4817.49657 4806.52627 10.97030 > 3.84150 1 YES! 0.000926
## C50AGE-3 PVAL 4817.49657 4811.26331 6.23326 > 3.84150 1 YES! 0.012537
## C50DIAG-2 PVAL 4817.49657 4810.21025 7.28632 > 5.99150 2 YES! 0.026170
## C50SEX-2 PVAL 4817.49657 4812.85533 4.64124 > 3.84150 1 YES! 0.031213
## C50WT-2 PVAL 4817.49657 4810.32347 7.17310 > 3.84150 1 YES! 0.007400
## NORMALAGE-2 PVAL 4817.49657 4810.18411 7.31245 > 3.84150 1 YES! 0.006848
## NORMALSEX-2 PVAL 4817.49657 4811.63157 5.86499 > 3.84150 1 YES! 0.015445
## NORMALWT-2 PVAL 4817.49657 4812.08371 5.41286 > 3.84150 1 YES! 0.019989
## T50AGE-3 PVAL 4817.49657 4808.20832 9.28825 > 3.84150 1 YES! 0.002306
## T50DIAG-2 PVAL 4817.49657 4810.30762 7.18895 > 5.99150 2 YES! 0.027475
## T50WT-2 PVAL 4817.49657 4807.36205 10.13451 > 3.84150 1 YES! 0.001455
##
## Parameter-covariate relation chosen in this forward step: BASE-WT-2
## CRITERION PVAL < 0.05
## BASE_MODEL_OFV 4817.49657
## CHOSEN_MODEL_OFV 4806.52627
## Relations included after this step:
## BASE WT-2
## C50 AGE-2
## NORMAL DIAG-2
## T50 AGE-2 SEX-2
## --------------------
##
## Model directory /green/home/USER/estch718/isop_covariates/models/scm_run14/forward_scm_dir1/scm_dir1/scm_dir1/scm_dir1/scm_di
##
## MODEL TEST BASE OFV NEW OFV TEST OFV (DROP) GOAL dDF SIGNIFICANT PVAL
## BASEAGE-2 PVAL 4806.52627 4804.62739 1.89888 > 3.84150 1 0.168200
## BASEDIAG-2 PVAL 4806.52627 4806.26918 0.25709 > 5.99150 2 0.879370
## BASESEX-2 PVAL 4806.52627 4803.94117 2.58510 > 3.84150 1 0.107870
## BASEWT-3 PVAL 4806.52627 4806.20029 0.32598 > 3.84150 1 0.568040
## C50AGE-3 PVAL 4806.52627 4821.39555 -14.86928 > 3.84150 1 9999
## C50DIAG-2 PVAL 4806.52627 4803.09786 3.42841 > 5.99150 2 0.180110
## C50SEX-2 PVAL 4806.52627 4806.13601 0.39027 > 3.84150 1 0.532160
## C50WT-2 PVAL 4806.52627 4804.95121 1.57506 > 3.84150 1 0.209470
## NORMALAGE-2 PVAL 4806.52627 4804.05143 2.47484 > 3.84150 1 0.115680
## NORMALSEX-2 PVAL 4806.52627 4806.35661 0.16966 > 3.84150 1 0.680410
## NORMALWT-2 PVAL 4806.52627 4805.41412 1.11215 > 3.84150 1 0.291620
## T50AGE-3 PVAL 4806.52627 4814.38508 -7.85881 > 3.84150 1 9999
## T50DIAG-2 PVAL 4806.52627 4804.45764 2.06864 > 5.99150 2 0.355470
## T50WT-2 PVAL 4806.52627 4802.43554 4.09073 > 3.84150 1 YES! 0.043119
##
## Parameter-covariate relation chosen in this forward step: T50-WT-2
## CRITERION PVAL < 0.05
## BASE_MODEL_OFV 4806.52627
## CHOSEN_MODEL_OFV 4802.43554
## Relations included after this step:
## BASE WT-2
## C50 AGE-2
## NORMAL DIAG-2
## T50 AGE-2 SEX-2 WT-2
## --------------------
##
## Model directory /green/home/USER/estch718/isop_covariates/models/scm_run14/forward_scm_dir1/scm_dir1/scm_dir1/scm_dir1/scm_di
##
## MODEL TEST BASE OFV NEW OFV TEST OFV (DROP) GOAL dDF SIGNIFICANT PVAL
## BASEAGE-2 PVAL 4802.43554 4802.08290 0.35264 > 3.84150 1 0.552620
## BASEDIAG-2 PVAL 4802.43554 4802.77135 -0.33581 > 5.99150 2 9999
## BASESEX-2 PVAL 4802.43554 4801.01227 1.42327 > 3.84150 1 0.232870
## BASEWT-3 PVAL 4802.43554 4798.94602 3.48952 > 3.84150 1 0.061759
## C50AGE-3 PVAL 4802.43554 4802.13061 0.30494 > 3.84150 1 0.580800
## C50DIAG-2 PVAL 4802.43554 4799.46007 2.97547 > 5.99150 2 0.225880
## C50SEX-2 PVAL 4802.43554 4802.25033 0.18521 > 3.84150 1 0.666930
## C50WT-2 PVAL 4802.43554 4802.28782 0.14772 > 3.84150 1 0.700720
## NORMALAGE-2 PVAL 4802.43554 4802.18536 0.25018 > 3.84150 1 0.616950
## NORMALSEX-2 PVAL 4802.43554 4803.01897 -0.58343 > 3.84150 1 9999
## NORMALWT-2 PVAL 4802.43554 4803.03235 -0.59681 > 3.84150 1 9999
## T50AGE-3 PVAL 4802.43554 4799.18664 3.24890 > 3.84150 1 0.071472
## T50DIAG-2 PVAL 4802.43554 4800.51755 1.91799 > 5.99150 2 0.383280
## T50WT-3 PVAL 4802.43554 4802.02665 0.40889 > 3.84150 1 0.522530
##
## --------------------
##
##
## --------------------
## Forward search done. Starting backward search inside forward top level directory
## Model directory /green/home/USER/estch718/isop_covariates/models/scm_run14/backward_scm_dir1/m1
##
## MODEL TEST BASE OFV NEW OFV TEST OFV (DROP) GOAL dDF INSIGNIFICANT PVAL
## BASEWT-1 PVAL 4802.43554 4816.49239 -14.05684 > -6.63490 -1 0.000177
## C50AGE-1 PVAL 4802.43554 4826.36049 -23.92495 > -6.63490 -1 0.000001
## NORMALDIAG-1 PVAL 4802.43554 4874.50948 -72.07394 > -9.21030 -2 2.24e-16
## T50AGE-1 PVAL 4802.43554 4845.45767 -43.02213 > -6.63490 -1 5.41e-11
## T50SEX-1 PVAL 4802.43554 4848.49816 -46.06262 > -6.63490 -1 1.15e-11
## T50WT-1 PVAL 4802.43554 4819.83165 -17.39611 > -6.63490 -1 0.000030
##
## --------------------
B.12 FREM
B.12.1 相关性型矩阵(Correlation matrix)
xpdb28 <- xpose::xpose_data(runno = 28, dir="models") # Read model output
prm28 <- xpose::get_prm(xpdb28) # Get final estimates
omg28 <- data.frame( prm28 %>% # Extract omega values
filter(type %in% c("ome")) %>% select(value, name))
lab <- data.frame( prm28 %>% # Get omega matrix labels
filter(type %in% c("ome"),
!label %in% "" ) %>% select(label))
labs <- as.character(unique(lab$label))
mat <- matrix(0, nrow = 8, ncol = 8) # Create empty omega matrix mat[upper.tri(mat, diag = TRUE)] <- omg28$value # Fill upper triangle mat <- t(mat) # Inverse matrix to get lower triangle
rownames(mat) <- lab$label # Assign names to the matrix
colnames(mat) <- lab$label
diag(mat) <- gsub(".*_", "", lab$label) # Assign names to the diagonal
dfmat <- melt(mat) # Melt for plotting
dfmat$text <- as.numeric(dfmat$value) # Create info for plot text
dfmat$text <- ifelse(is.na(dfmat$text), dfmat$value,
ifelse(dfmat$text == 0, "", round(dfmat$text, 2))) dfmat$text <- ifelse( # Prettify for long name
dfmat$text %in% c("NORMAL"), " NORMAL", dfmat$text) dfmat$value <- as.numeric(dfmat$value)
ggplot(dfmat, aes(x = Var2, y= Var1, fill = value)) + geom_tile(color = "white") +
geom_text(aes(label = text)) +
geom_regon(aes(x0 = 2.5, y0 = 6.5, sides = 4, angle = 0, r= 2.8, color="Parameter-parameter correlation"), size=0.5, alpha=0)+
geom_regon(aes(x0 = 2.5, y0 = 2.5, sides = 4, angle = 0, r= 2.8, color="Parameter-covariate correlation"), size=0.5, alpha=0)+
geom_regon(aes(x0 = 6.5, y0 = 2.5, sides = 4, angle = 0, r= 2.8, color="Covariate-covariate correlation"), size=0.5, alpha=0)+
scale_fill_gradient2( na.value = "white", low = "blue", high = "red", mid = "white", midpoint = 0, limit = c(-1.01, 1.01)) +
theme_minimal() +
# coord_fixed() +
scale_x_discrete(limits=labs) + # Flip the x axis
scale_y_discrete(limits=labs[length(labs):1]) +
theme(
axis.text = element_blank(),
axis.title.x = element_blank(),
axis.title.y = element_blank(),
panel.grid.major = element_blank(),
panel.border = element_blank(), panel.background = element_blank(), axis.ticks = element_blank(),
# legend.position = "top"#,
# legend.direction = "horizontal"
) +
guides(fill = guide_colorbar(
# barwidth = 7, barheight = 4, title.position = "top", title.hjust = 0.5,
title = "Correlation value"), color = guide_legend(""))
B.12.2 森林图(Forest plot)
• 从PsN输出的文件夹中导入数据
frem <- read.csv( # Get post processing info from PsN after running frem
"models/frem_run11/results.csv", fill = TRUE,
col.names = paste0("V", seq_len(8)), header = F
)
# Data management
frem$tbl_id <- # Add unique ID for the different tables
cumsum(frem$V2 == "")
cov_coef <- # Select lines with info for forest plots
frem[frem$tbl_id == 3, ] %>% slice(-1) %>%
select(1:6) names(cov_coef) <-
lapply(cov_coef[1,], as.character) # rename columns
cov_unex <- # Select lines with info for unexplained variability plots
frem[frem$tbl_id == 5, ] names(cov_unex) <-
lapply(cov_unex[2,], as.character) # rename columns
cov_unex <- cov_unex[-c(1, 2), ]
cov_stat <- # Select lines with cov stat info
frem[frem$tbl_id == 6, ] names(cov_stat) <-
lapply(cov_stat[2,], as.character) # rename columns
cov_stat <- cov_stat[-c(1, 2), ] %>%
mutate(`5th` = p5, `95th` = p95) %>% # Get long format
select(covariate, `5th`, `95th`, other) %>%
gather(key = "condition", value = "cov_stat", `5th`, `95th`, other)
• 森林图
cov <- merge(cov_coef, cov_stat) # Merge cov stat and cov coefficients and uncertainty
cov_p <- cov %>%
mutate_at(list(as.character), .vars = vars(2, 4:6)) %>% # Format to numerics
mutate_at(vars(4:6), list(as.numeric)) %>%
mutate(
rp5 = p5 * 100- 100,
rp95 = p95 * 100- 100,
rmean = mean * 100- 100
) %>% # Convert to % and normalize to 0
mutate(covariate = recode(
covariate,
AGE = "Age",
SEX = "Sex",
WT = "Weight",
DIAG_2 = "COPD",
DIAG_3 = "COPD and asthma"
),
parameter = recode(
parameter,
BASE = "Base",
NORMAL = "Normal",
C50 = "C50",
T50 = "T50"
)) %>% # Rename
mutate(condition = fct_relevel(condition, "other", "95th", "5th")) %>% # Reorder
mutate(covariate = fct_relevel(covariate, "Age", "Weight", "COPD", "COPD and asthma", "Sex"))
cov_p <- cov_p %>% # Remove infinite values from the plot
mutate(rmean = ifelse(rmean > 2e+20, NA, rmean),
rp5 = ifelse(rp5 > 2e+20, NA, rp5),
rp95 = ifelse(rp95 > 2e+20, NA, rp95))
p1 <-
ggplot(data = cov_p[cov_p$parameter %in% c("Base"), ],
aes(
y = condition,
x = rmean,
xmin = rp5,
xmax = rp95,
label = cov_stat
)) +
geom_point() +
facet_grid(covariate~., scale="free", labeller = label_wrap_gen(width=3))+
geom_vline(xintercept=0, color="black", linetype="dashed", alpha=.5)+
geom_vline(xintercept=-20, color="black", linetype="dotted", alpha=.5)+
geom_vline(xintercept=+20, color="black", linetype="dotted", alpha=.5)+
theme_bw()+
geom_text(nudge_y = 0.4, size=2) +
scale_x_continuous( name=NULL)+
scale_y_discrete( name="Base")+
geom_errorbarh(height=.1) + #adds the CIs
force_panelsizes() +
theme(text = element_text(size=8))
p2 <-
ggplot(data = cov_p[cov_p$parameter %in% c("Normal"), ],
aes(
y = condition,
x = rmean,
xmin = rp5,
xmax = rp95,
label = cov_stat
)) +
geom_point() +
facet_grid(covariate~., scale="free", labeller = label_wrap_gen(width=1.5))+
geom_vline(xintercept=0, color="black", linetype="dashed", alpha=.5)+
geom_vline(xintercept=-20, color="black", linetype="dotted", alpha=.5)+
geom_vline(xintercept=+20, color="black", linetype="dotted", alpha=.5)+
theme_bw()+
geom_text(nudge_y = 0.4, size=2) +
scale_x_continuous( name=NULL)+
scale_y_discrete( name="Normal")+
geom_errorbarh(height=.1)+ #adds the CIs
force_panelsizes() +
theme(text = element_text(size=8))
p3 <-
ggplot(data = cov_p[cov_p$parameter %in% c("T50"), ],
aes(
y = condition,
x = rmean,
xmin = rp5,
xmax = rp95,
label = cov_stat
)) +
geom_point() +
facet_grid(covariate~., scale="free", labeller = label_wrap_gen(width=3))+
geom_vline(xintercept=0, color="black", linetype="dashed", alpha=.5)+
geom_vline(xintercept=-20, color="black", linetype="dotted", alpha=.5)+
geom_vline(xintercept=+20, color="black", linetype="dotted", alpha=.5)+
theme_bw()+
geom_text(nudge_y = 0.4, size=2) +
scale_x_continuous( name=NULL)+
scale_y_discrete( name="T50")+
geom_errorbarh(height=.1) + #adds the CIs
force_panelsizes() +
theme(text = element_text(size=8))
p4 <-
ggplot(data = cov_p[cov_p$parameter %in% c("C50"), ],
aes(
y = condition,
x = rmean,
xmin = rp5,
xmax = rp95,
label=cov_stat
)) +
geom_point()+
facet_grid(covariate~.,scale="free",labeller=label_wrap_gen(width=2))+
geom_vline(xintercept=0,color="black",linetype="dashed",alpha=.5)+
geom_vline(xintercept=-20,color="black",linetype="dotted",alpha=.5)+
geom_vline(xintercept=+20,color="black",linetype="dotted",alpha=.5)+
theme_bw()+
force_panelsizes()+
geom_text(nudge_y=0.4,size=2) +
scale_x_continuous(name=NULL)+
scale_y_discrete(name="C50")+
geom_errorbarh(height=.1)+#addstheCIs
theme(text=element_text(size=8))
gridExtra::grid.arrange(p1,p2,p3,p4, nrow=2,
bottom="Effectsizeinpercent")
B.12.3 无法解释的变异(Unexplained variability)
cov_u <- cov_unex %>% select(1:5) %>%
mutate_at(list(as.character), .vars = vars(3:5)) %>% # Convert to numerics
mutate_at(vars(3:5), list(as.numeric)) %>% mutate( # Rename
covariate = recode( covariate,
none = "None", all = "All", AGE = "Age", SEX = "Sex",
WT = "Weight", DIAG_2 = "COPD",
DIAG_3 = "COPD and asthma"
),
parameter = recode( parameter,
BASE = "Base",
NORMAL = "Normal", C50 = "C50",
T50 = "T50"
)
) %>%
mutate(covariate = fct_relevel(covariate, # Reorder
"All", "Age", "Weight", "COPD", "COPD and asthma", "Sex", "None"))
ggplot(data = cov_u,
aes(
y = covariate,
x = sd_observed, xmin = sd_5th, xmax = sd_95th
)) +
geom_point() +
facet_wrap(parameter ~ ., scale = "free") + theme_bw() +
scale_x_continuous(name = "Standard deviation of unexplained variability") + scale_y_discrete(name = "Covariate") +
geom_errorbarh(height = .1) #adds the CIs
B.13 森林图(Forest plots)
xpdb20 <- xpose::xpose_data(runno=20, dir="models/") prm20f <- xpose::get_prm(xpdb20)
prm20f$se <- # Values from SIR
c(8.75124, 29.85375, 5.166212, 2.273961, 0.07364673,
0.7777551, 0.03512398, 0.04976547, 0.001446226,
0.04206618, 0.009734037, 0.6732954, 0.268544, 0.003135913)
prmp <- prm20f %>%
filter(type %in% c("the"), # Select only covariates effects
!grepl("TV_", label) ) %>% select(label, value, se)
for (i in c(20,75)){ # Covariate effect at different ages
prmp <- prmp %>% slice(rep(3,1)) %>%
mutate(label = paste0("Age ", i, " years"), value = value * (i - 40),
se = se * (i - 40)) %>% # SE value from SIR
add_row(., .before=1, prmp)
}
for (i in c(2,3)){ # Covariate effect for the DIAG categories
prmp <- prmp %>% slice(rep(1,1)) %>%
mutate(label = ifelse(i == 1, "Asthma",
ifelse(i == 2, "COPD",
"COPD and Asthma")), value = value * (1 - i),
se = se * (1 - i)) %>% add_row(., .before=1, prmp)
}
prmp %>% # Create the plot
filter(!label %in% c("FYEARS", "DIAG")) %>%
mutate( ci5 = 1 + (value - 1.96*se), # Get the 95 CI
ci95 = 1 + (value + 1.96*se),
value = 1 + value, # Covariate equation
nb = ifelse(value < 1, paste0(round(value, 3), " [", # Text
round(ci5, 3), " - ",
round(ci95, 3), "]"),
paste0(round(value, 3), " [",
round(ci95, 3), " - ",
round(ci5, 3), "]"))) %>% ggplot(., aes( y= label, x= value,
xmin = ci5, xmax = ci95 )) + geom_point(aes(color = label), shape=3) + geom_errorbarh(aes(color = label), height=.1) +
geom_vline(xintercept=1, color="black", linetype="dashed", alpha=.5)+ geom_text(aes(label=nb, x= 1.5), hjust = 0) +
scale_x_continuous( name="Covariate effect on Normal",
limits = c(0.35,2)) + scale_y_discrete( name=NULL) +
theme_bw() + theme(legend.position = "none")
B.14 VPCs
B.14.1 默认的可视化预测检验(Default VPCs)
图S16中左侧面板的默认的可视化预测检验
• PsN命令:
vpc run11.mod -samples=500 -auto_bin=auto -rplots=1 -dir=run11_vpc_n500
• R代码:
vpc <- function(n) { # Function to create non stratified VPC
xpdb <- # Read model information from PsN model folder
xpose::xpose_data(runno = n, dir = "models")
p <- vpc::vpc(
psn_folder = paste0("models/run", n, "_vpc_n500"), show = c(
obs_dv = T, sim_median = T, pi = T
),
pi = c(0.05, 0.95),
ci = c(0.025, 0.975),
xlab = "Time (h)", ylab = "PEFR (L/min)", title = NULL,
vpc_theme = vpc::new_vpc_theme( update = list(
obs_shape = ".", obs_median_color = "black", obs_median_linetype = "solid", obs_median_size = 0.5, obs_ci_color = "#3388cc", obs_ci_linetype = "solid",
sim_pi_linetype = 'dashed',
sim_pi_size = 0.5, sim_pi_color = "#3388cc", sim_median_fill = "black", sim_median_color = "black",
sim_median_linetype = "dashed", sim_median_size = 0.5
)
)
) + theme_bw() +
scale_x_continuous(limits = c(0, 450)) + scale_y_continuous(limits = c(0, 900))
return(p)
}
vpc11 <- vpc(11) + # Create VPC for run n
labs(subtitle = "Model without covariates (run11)")
vpc25 <- vpc(25) +
labs(subtitle = "Covariate model from SCM (run25)", y= NULL)
grid.arrange(vpc11, vpc25, ncol = 2)
B.14.2 分层的可视化预测检验(Stratified VPCs)
将连续协变量转化为二分类以分层绘制可视化预测检验图 S17.
• PsN命令:
vpc run110.mod -samples=500 -auto_bin=auto -stratify_on=AGEC -rplots=1 -dir=run110_vpc_n500_stratAGEC
• 添加到 NONMEM 代码行以用于将连续协变量转化为二分类变量:
> AGEC=0
> IF(AGE.GT.34)AGEC=1
> $TABLE ID TIME SEX DIAG AGEC YNOPRINT ONEHEADER FILE=catab110
• R代码:
lab <- # Custom strip labels
c("0" = "AGE =< 34 years", "1" = "AGE > 34 years")
vpc_strat <- function(n, cov) { # VPC function with stratification
xpdb <- # Read model information from PsN model folder
xpose::xpose_data(runno = n, dir = "models")
p <- vpc::vpc(
psn_folder = paste0("models/run", n, "_vpc_n500_strat", cov), show = c(
obs_dv = T, sim_median = T, pi = T
),
stratify = c(cov), facet = "rows",
labeller = labeller(AGEC = lab), pi = c(0.05, 0.95),
ci = c(0.025, 0.975),
xlab = "Time (h)", ylab = "PEFR (L/min)", title = NULL,
vpc_theme = vpc::new_vpc_theme( update = list(
obs_shape = ".", obs_median_color = "black", obs_median_linetype = "solid", obs_median_size = 0.5, obs_ci_color = "#3388cc", obs_ci_linetype = "solid",
sim_pi_linetype = 'dashed',
sim_pi_size = 0.5, sim_pi_color = "#3388cc", sim_median_fill = "black", sim_median_color = "black",
sim_median_linetype = "dashed", sim_median_size = 0.5
)
)
) + theme_bw() +
scale_x_continuous(limits = c(0, 450)) + scale_y_continuous(limits = c(0, 950))
return(p)
}
vpc110 <- vpc_strat(110, "AGEC") +
labs(subtitle = "Model without covariates (run11)", x = NULL)
vpc250 <- vpc_strat(250, "AGEC") +
labs(subtitle = "Covariate model from SCM (run25)")
grid.arrange(vpc110, vpc250, ncol = 1)
B.14.3 使用协变量最为作为自变量的可视化预测检验(VPCs using a covariate as independent variable)
使用协变量最为作为自变量的可视化预测检验 (图 S18)
• PsN 命令:
vpc run11.mod -samples=500 -auto_bin=auto -idv=AGE -rplots=1 -dir=run11_vpc_n500_idvAGE
• R 代码:
vpc <- function(n) { # Function to create non stratified VPC
xpdb <- # Read model information from PsN model folder
xpose::xpose_data(runno = n, dir = "models")
p <- vpc::vpc(
psn_folder = paste0("models/run", n, "_vpc_n500_idvAGE"),
obs_cols = list(idv="AGE"),
sim_cols = list(idv="AGE"),
show = c(
obs_dv = T,
sim_median = T,
pi = T
),
pi = c(0.05, 0.95),
ci = c(0.025, 0.975),
xlab = "Age (year)",
ylab = "PEFR (L/min)",
title = NULL,
vpc_theme = vpc::new_vpc_theme(
update = list(
obs_shape = ".",
obs_median_color = "black",
obs_median_linetype = "solid",
obs_median_size = 0.5,
obs_ci_color = "#3388cc",
obs_ci_linetype = "solid",
sim_pi_linetype = 'dashed',
sim_pi_size = 0.5,
sim_pi_color = "#3388cc",
sim_median_fill = "black",
sim_median_color = "black",
sim_median_linetype = "dashed",
sim_median_size = 0.5
)
)
) + theme_bw() +
scale_y_continuous(limits = c(0, 850))
return(p)
}
vpc11 <- vpc(11) +
labs(subtitle = "Model without covariates (run11)")
vpc25 <- vpc(25) +
labs(subtitle = "Covariate model from SCM (run25)", y = NULL)
grid.arrange(vpc11, vpc25, ncol = 2)
C 添加包与环境(Libraries and environment)
## R version 4.1.2 (2021-11-01)
## Platform: x86_64-apple-darwin17.0 (64-bit)
## Running under: macOS Big Sur 10.16
##
## Matrix products: default
## BLAS: /Library/Frameworks/R.framework/Versions/4.1/Resources/lib/libRblas.0.dylib
## LAPACK: /Library/Frameworks/R.framework/Versions/4.1/Resources/lib/libRlapack.dylib
##
## locale:
## [1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
##
## attached base packages:
## [1] stats graphics grDevices utils datasets methods base
##
## other attached packages:
## [1] xpose_0.4.13 forcats_0.5.1 stringr_1.4.0 readr_2.1.0
## [5] tidyr_1.1.4 tibble_3.1.6 tidyverse_1.3.1 summarytools_1.0.0
## [9] reshape2_1.4.4 purrr_0.3.4 PsNR_0.2.0 plyr_1.8.6
## [13] patchwork_1.1.1 knitr_1.36 kableExtra_1.3.4 huxtable_5.4.0
## [17] ggh4x_0.2.1 ggpubr_0.4.0 ggiraphExtra_0.3.0 ggiraph_0.7.10
## [21] ggforce_0.3.3 GGally_2.1.2 ggplot2_3.3.5 gtsummary_1.5.0
## [25] ftExtra_0.2.0 dplyr_1.0.7 data.table_1.14.2
##
## loaded via a namespace (and not attached):
## [1] colorspace_2.0-2 ggsignif_0.6.3 pryr_0.1.5
## [4] ellipsis_0.3.2 sjlabelled_1.1.8 flextable_0.6.10
## [7] fs_1.5.0 base64enc_0.1-3 rstudioapi_0.13
## [10] farver_2.1.0 bit64_4.0.5 fansi_0.5.0
## [13] lubridate_1.8.0 xml2_1.3.2 codetools_0.2-18
## [16] splines_4.1.2 sjmisc_2.8.7 polyclip_1.10-0
## [19] jsonlite_1.7.2 gt_0.3.1 broom_0.7.10
## [22] dbplyr_2.1.1 compiler_4.1.2 httr_1.4.2
## [25] backports_1.3.0 assertthat_0.2.1 Matrix_1.3-4
## [28] fastmap_1.1.0 cli_3.1.0 tweenr_1.0.2
## [31] htmltools_0.5.2 tools_4.1.2 gtable_0.3.0
## [34] glue_1.5.0 Rcpp_1.0.7 carData_3.0-4
## [37] cellranger_1.1.0 vctrs_0.3.8 svglite_2.0.0
## [40] nlme_3.1-153 broom.helpers_1.4.0 insight_0.14.5
## [43] xfun_0.28 rvest_1.0.2 lifecycle_1.0.1
## [46] rstatix_0.7.0 MASS_7.3-54 scales_1.1.1
## [49] vroom_1.5.6 hms_1.1.1 parallel_4.1.2
## [52] mycor_0.1.1 RColorBrewer_1.1-2 yaml_2.2.1
## [55] pander_0.6.4 gdtools_0.2.3 reshape_0.8.8
## [58] stringi_1.7.5 checkmate_2.0.0 ppcor_1.1
## [61] zip_2.2.0 commonmark_1.7 rlang_0.4.12
## [64] pkgconfig_2.0.3 systemfonts_1.0.2 matrixStats_0.61.0
## [67] evaluate_0.14 lattice_0.20-45 rapportools_1.0
## [70] htmlwidgets_1.5.4 bit_4.0.4 tidyselect_1.1.1
## [73] magrittr_2.0.1 bookdown_0.24 R6_2.5.1
## [76] magick_2.7.3 generics_0.1.1 DBI_1.1.1
## [79] pillar_1.6.4 haven_2.4.3 withr_2.4.2
## [82] mgcv_1.8-38 abind_1.4-5 modelr_0.1.8
## [85] crayon_1.4.2 car_3.0-12 uuid_1.0-3
## [88] utf8_1.2.2 tzdb_0.2.0 rmarkdown_2.11
## [91] officer_0.4.1 grid_4.1.2 readxl_1.3.1
## [94] reprex_2.0.1 digest_0.6.28 webshot_0.5.2
## [97] munsell_0.5.0 viridisLite_0.4.0 tcltk_4.1.2
附件二：
组合协变量关系的示例
协变量模型通常由多个单独的协变量效应通过相乘进行组合而成。如果协变量效应是根据标准协变量值定义的，当协变量具有标准值时，协变量效应的值为 1，则群体参数值$CL_{pop}$将表示标准个体的值，例如 70 公斤、176 厘米、年龄 40 岁、肾功能正常、男性。预测参数$CL_{grp}$描述了一组具有相同协变量的受试者的典型参数。
$$ CL_{grp}= CL_{pop} \times fsize \times fmat \times fof \times fgeno \times fconmed \tag{方程 1} $$其中
$$ fsize=(\frac{NFM}{NFMstd})^{3/4} \tag{方程 2} $$ $$ fmat=(\frac{1}{1+(\frac{PMA}{Tmat50})^{-HillMat}}) \tag{方程 3} $$ $$ fof=\frac{CLcr}{CLcrstd} \tag{方程 4} $$$fgeno$ = if $sex$==$female$ then $Ffemale$ else $1$ (方程 5)
$fconmed$ = if $conmed$ == $amiodarone$ then $Famio$ else $1$ (方程 6)
体型大小的协变量函数fsize表示使用标准个体（总体重70公斤，身高176厘米，男性）的NFM标准化后的个体正常脂肪量（NFM）。它被嵌入到一个幂函数中，使用一个基于理论的适合于清除率的异速缩放指数。
对于新生儿、婴儿和幼儿来说，器官成熟的影响fmat可以用sigmoid模型来描述，该模型包括成熟半衰Tmat50、成熟陡峭因子HillMat和月经后年龄 PMA（通常以周为单位表示）。使用标准肌酐清除率CLcr对个体的CLcr进行标准化用于表示肾功能，表示器官功能效应，即器官功能协变量fof。由于器官功能通常随着体型大小和成熟而变化，因此应调整器官功能的标准值，使其与CLcr预测值中隐含的大小和成熟度一致，例如，利用肾小球滤过率的大小和成熟开发[1]。基因型函数 fgeno ，用性别来说明。当性别为女性时，该函数已通过参数 Ffemale 预测。伴随药物，如fgeno，通常是分类的，但也可能是剂量的函数。
清除率可以被分为两个或多个组分，每个组分可以有自己的一组协变量函数，例如，可以使用肾器官功能$fof_{rf}$来区分与肾功能相关联的分量$CL_{rf}$和与肾功能无关的分量$CL_{nrf}$。所有清除率组分可能共享与公式 7 所示相同的体型大小函数，但这不是必需的。
$$ \small{CL_{grp}=\left( \begin{align} CL_{nrf} \times fmat_{nrf} \times fof_{nrf} \times fgeno \times fconmed \\ + CL_{rf} \times fmat_{rf} \times fof_{rf} \end{align} \right)} \tag{方程 7} $$参考文献(中文翻译):
- Rhodin, M.M., et al., 人类肾脏功能成熟：使用体重和经后年龄的定量描述。Pediatric nephrology, 2009. 24(1): p. 67-76.
参考文献(英文原文):
- Rhodin, M.M., et al., Human renal function maturation: a quantitative description using weight and postmenstrual age. Pediatric nephrology, 2009. 24(1): p. 67-76.