前言：

本案例介绍如何使用PML（Phoenix建模语言）轻松构建出多种对S形曲线及进行拟合的模型。

使用的数据：

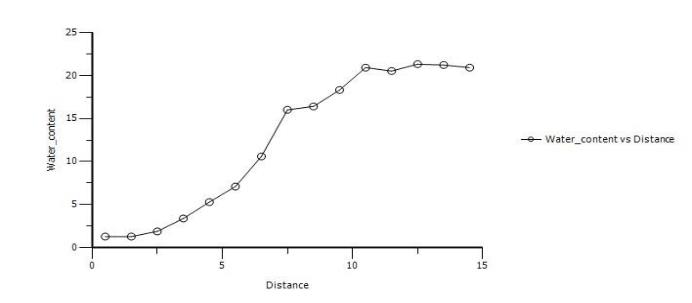
数据取自由Heyes和Brown的报告的叶子的生长数据（1956）。

含水量对距离散点图如下，可以看到生成的图形是S形的:

目的：

使用下述的一系列S形模型拟合数据：

• Logistic(逻辑分布累计分布曲线)
• Gompertz(戈珀兹曲线)
• Weibull(韦伯分布累计分布曲线)
• Richards(Richards增长曲线)
• Morgan-Mercer-Flodin
• Hill(希尔方程)

通过该案例展示Phoenix Model操作对象在参数名称和方程方面的灵活性。

• 为方便起见, 所有模型都参数化α, β, γ, δ。

具体模型的介绍与实现：

1.Logistic模型和方程

特点：

• Logistic模型是最简单的S形模型。
• 下渐近线为0，上渐近线为Y的最大值.
• 该模型关于拐点是对称的。
• 应该用于模拟拐点大约是最大Y的1/2的过程。

方程：

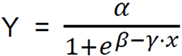
3个参数：

• α=曲线中Y的最大值
• β=曲线的中点
• γ=曲线的陡度

对应的PML代码：

2. Gompertz模型和方程

特点：

• Gompertz模型最初用于模拟人类死亡率，先验假设一个人的死亡抵抗力随着年龄的增长而降低。今天的应用实例包括精算科学和细菌生长曲线建模。
• 下渐近线为0，上渐近线为Y的最大值.
• 是广义Logistic函数的特例。其与Logistic函数的不同是S型两边不对称，拐点偏前。

方程：

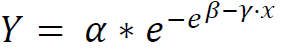
3个参数：

• α=曲线中Y的最大值
• β=生长速度b
• γ=生长速率c

对应的PML代码：

3. Weibull模型和方程

特点：

• 累积Weibull模型也称为“拉伸指数”函数。 它添加了一个参数delta，允许修改拐点。
• 上渐近线是Y的最大值，下渐近线可以是非零。
• 应用：通常用于在固体剂型溶解期间模拟粒度。

方程：

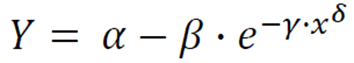
4个参数：

• α = 曲线中Y的最大值 (上部渐近线)
• β = 下渐近线
• γ = 控制拐点的 x 值
• δ = 曲线的陡峭度

对应的PML代码：

4.Richards模型和方程

特点：

• Richards模型对非对称S型曲线建模具有很强的灵活性。它还使用增量参数修改拐点。
• 上渐近线是最大 Y, 下渐近线可以是非零。
• 应用: 增长率曲线

方程：

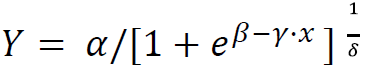
4个参数：

• α = 曲线的最大 Y 值 (上部渐近线)
• β = 生长速率
• γ = x 轴上的拐点
• δ = 控制拐点的 x 值

对应的PML代码：

5.Morgan-Mercer Flodin模型和方程

特点：

• Morgan-Mercer-Flodin模型首先用于模拟生物效率，例如对营养素存在的反应。允许不对称增长（即拐点不一定是1/2最大的）。
• 上渐近线是最大Y，下渐近线可以是非零。
• 应用：增长率曲线

方程：

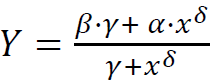
4个参数：

• α=曲线的最大Y值（上渐近线）
• β=增长率
• γ=增长率
• δ=控制拐点的x值

对应的PML代码：

6.Hill模型和方程

特点：

• Hill模型最初用于描述氧与血红蛋白结合的动力学。它现在被广泛用于模拟药效学。使用诸如Emax和EC50之类的参数名称，这是经典的sigmoid Emax模型。
• 指数gamma可用于修改拐点。 E0的加法允许Y截距为非零。
• 上渐近线是最大Y，下渐近线可以是非零。

方程：

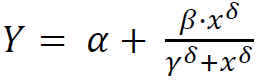
4个参数：

• α=下渐近线（E0）
• β=上渐近线（Emax）
• γ=拐点的x值（EC50）
• δ=指数控制曲线的陡度（n）

对应的PML代码：

对应的Phoenix Model中的内置模型：

带有基线的S型Emax模型

对应的使用药效学参数命名的PML代码：

使用药效学Emax模型参数估算初值估算技巧估算当前Hill方程参数初值：

• E0 = 1，来自X = 0处的探索图
• Emax = 20，来自X = 20的探索图
• EC50 = 10，来自½Emax
• N =指数任意设定为1（来自简化模型）

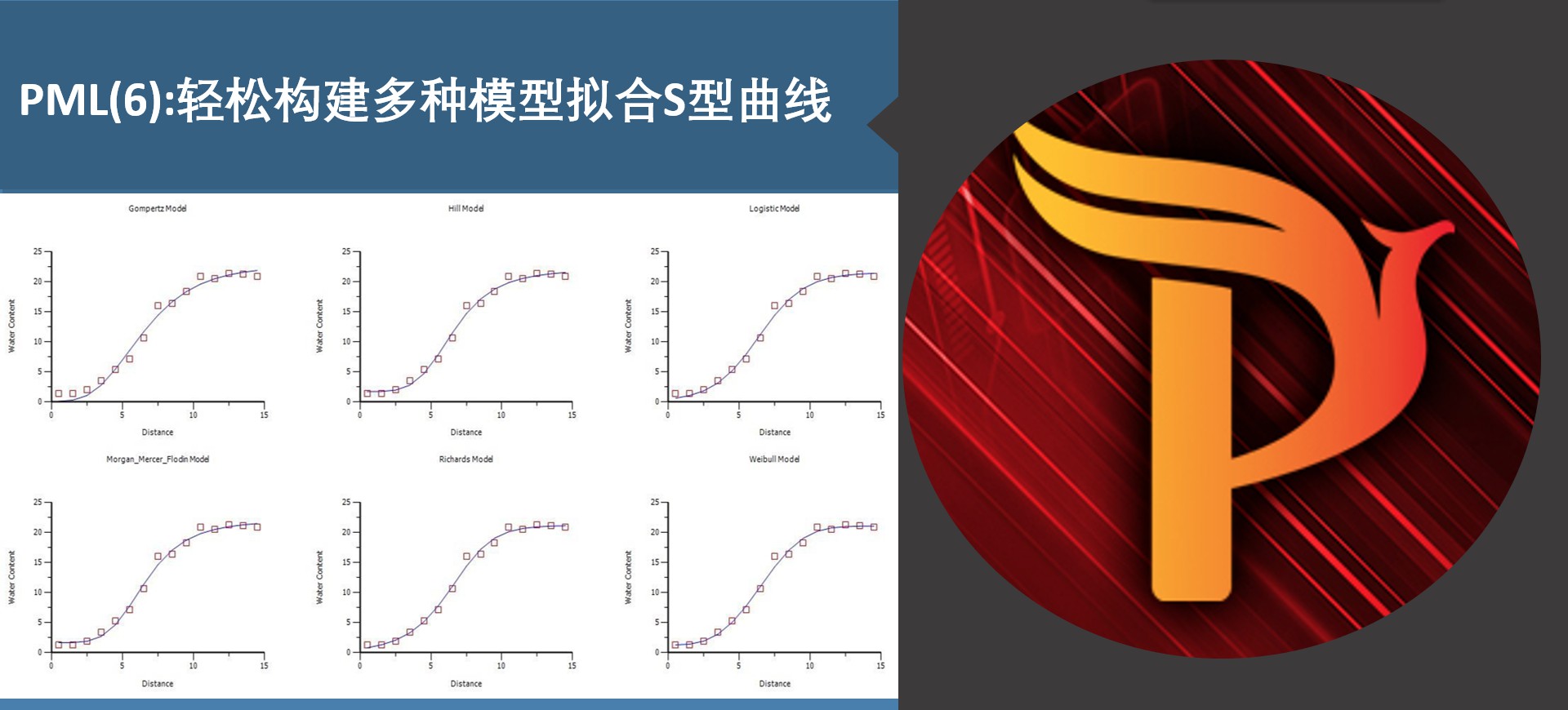
结果：

所有模型的观察和预测(水分含量)对距离图：

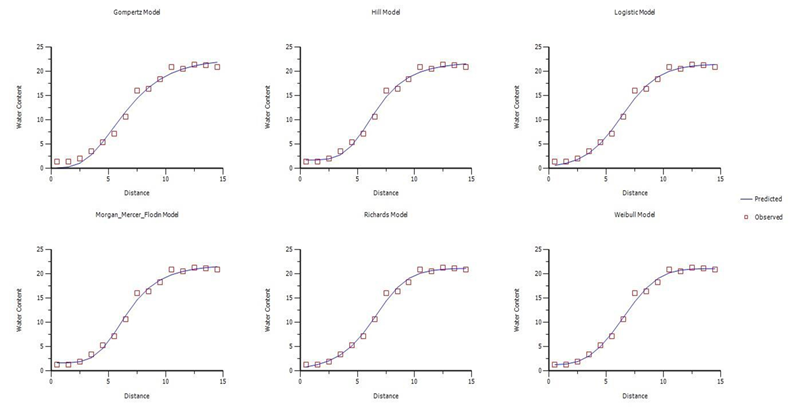
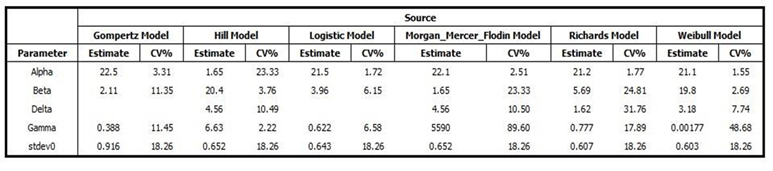
模型参数估计值（Theta）表格比较：

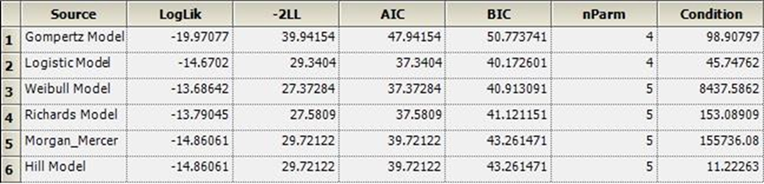
信息判据（Overall）表格比较：

参考文献：

Gabrielsson、药动学和药效学数据分析：概念和应用, 第五版,(2015)，PD11案例。