生物统计视角的PopPK
付永超 / 2020-10-12
群体药物代谢动力学是生物统计与药物代谢动力学的交叉学科,过往大家多从药物代谢动力学的视角介绍PopPK,今天我尝试通过生物统计学的统计模型视角介绍Pop PK,以便生物统计学家可以快速理解Pop PK,以及帮助大家更好的多视角立体的看待Pop PK。
介绍流程
1.使用Phoenix软件,基于一个群体模型模拟出一组数据。
2.群体分析常用的三种方法,单纯积聚法,两步法,一步法
3.尝试应用Phoenix中的用于生物统计的“线性混合效应(Linear Mixed Effect)”操作对象,和用于PopPK建模的“最大似然模型(ML Model)”操作对象,实现这三种方法,并对比操作设置与计算结果。
1. 使用Phoenix软件,基于一个群体模型模拟出一组数据。
1.1模拟所使用的模型
PK模型:
-
静脉注射,一房室,线性消除
-
使用V、ke参数化模型
变异假设:
-
残差(个体内变异)变异:对数加和型误差
-
个体内变异:仅考虑V的个体变异,V为对数正态分布
参数值:
-
表观分布容积的典型值,tvV=10,L
-
消除速率的典型值,tvke=0.1,1/h
-
残差(个体内变异)的方差,σ^2=0.09,
-
表观分布容积的个体间变异方差,𝜔_𝑉^2=0.09
1.2使用该模型模拟的原因
该模型浓度数据对数转换后,可以使用常见的线性模型拟合,来替代“PK模型”部分
1.3对数转换后可用的线性模型
Ln(Conc)=int+time* β+ε
其中
-
int,截距
-
β,斜率
-
ε,残差
-
time,时间
与PK参数的关系
-
V=Dose/C0=Dose/int
-
ke=- β
1.4模拟出的数据
| subject | time | C | DV | EXP_DV |
|---|---|---|---|---|
| 1.00 | 1.00 | 103.66 | 5.20 | 182.16 |
| 1.00 | 2.00 | 93.79 | 4.39 | 80.49 |
| 1.00 | 4.00 | 76.79 | 3.68 | 39.56 |
| 1.00 | 8.00 | 51.47 | 3.04 | 20.92 |
| 1.00 | 24.00 | 10.39 | 2.08 | 8.04 |
| 2.00 | 1.00 | 155.09 | 5.18 | 177.11 |
| 2.00 | 2.00 | 140.33 | 4.91 | 135.40 |
| 2.00 | 4.00 | 114.89 | 4.68 | 107.46 |
| 2.00 | 8.00 | 77.02 | 4.58 | 97.04 |
| 2.00 | 24.00 | 15.55 | 2.37 | 10.70 |
| 3.00 | 1.00 | 83.78 | 4.68 | 107.88 |
| 3.00 | 2.00 | 75.81 | 4.58 | 97.68 |
| 3.00 | 4.00 | 62.07 | 4.16 | 64.21 |
| 3.00 | 8.00 | 41.60 | 3.98 | 53.65 |
| 3.00 | 24.00 | 8.40 | 1.95 | 7.02 |
| 4.00 | 1.00 | 49.08 | 3.57 | 35.53 |
| 4.00 | 2.00 | 44.41 | 3.29 | 26.80 |
| 4.00 | 4.00 | 36.36 | 3.44 | 31.09 |
| 4.00 | 8.00 | 24.37 | 3.06 | 21.22 |
| 4.00 | 24.00 | 4.92 | 0.96 | 2.60 |
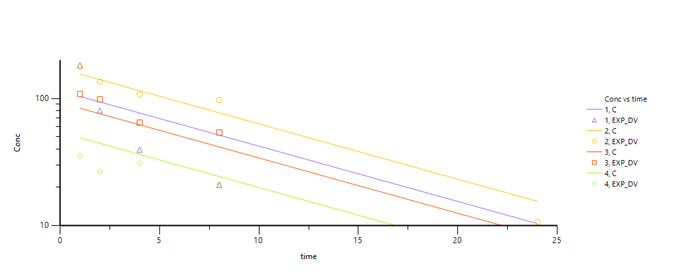
其中:
-
subject,个体编号
-
time,时间
-
C,个体浓度预测值
-
DV,对数转换后的个体浓度观测值
-
EXP_DV,未经对数转换的个体浓度观测值
2.群体药物代谢动力学分析常用的三种方法,单纯积聚法,两步法,一步法
2.1单纯积聚法
将同一时间浓度值之间的差异,都认为是残差变异,不考虑个体因素。
或者表述为,将所有个体是为一个个体。
2.2两步法
将个体是为一个分类变量,并将该变量认为是一个固定效应,估计个体因素的每个水平。
或者表述为,为每个个体分别拟合出其所对应的参数。
2.3一步法
将个体是为一个分类变量,并将该变量认为是一个随机效应,估计个体因素的均值与方差。
或者表述为,将一组个体认为是从一个统计总体中随机抽取出的一个样本,通过通过该样本去估计整个统计总体的参数(均值,方差)。
3.尝试应用Phoenix中的用于生物统计的“线性混合效应(Linear Mixed Effect)”操作对象,和用于PopPK建模的“最大似然模型(ML Model)”操作对象,实现这三种方法,并对比操作设置与计算结果。
3.1不考虑个体因素
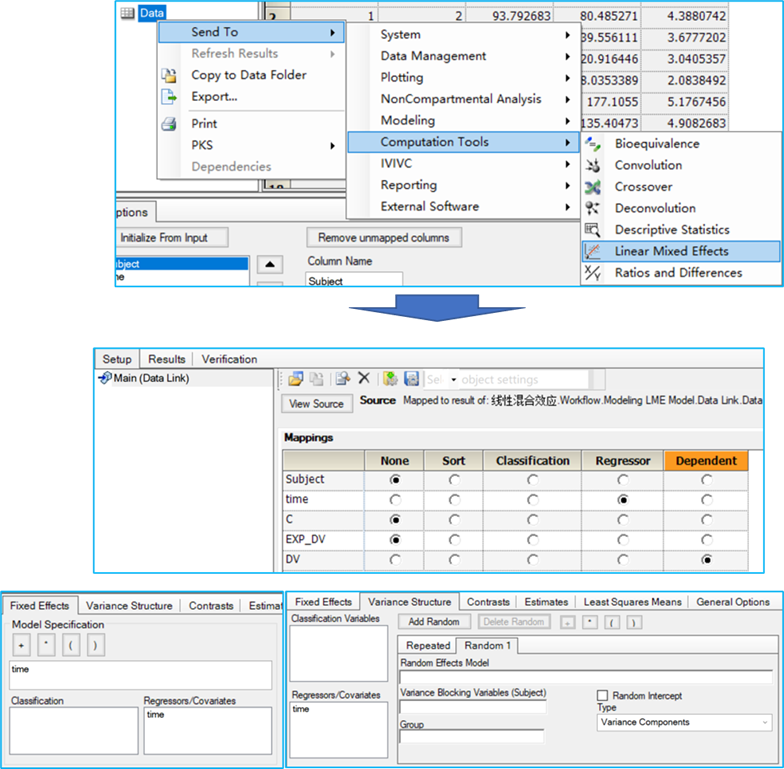
3.1.1LME模型构建
使用的统计学模型
Ln(Conc)=int+time* β+ε
Phoenix中的操作
-
将数据集发送至线性混合效应模型操作对象
-
将DV映射值“因变量(Dependent)”字段
-
将time映射至“回归字段(Regressor)”
-
在“固定效应(Fixed Effect)”选项卡,将time指定为固定效应
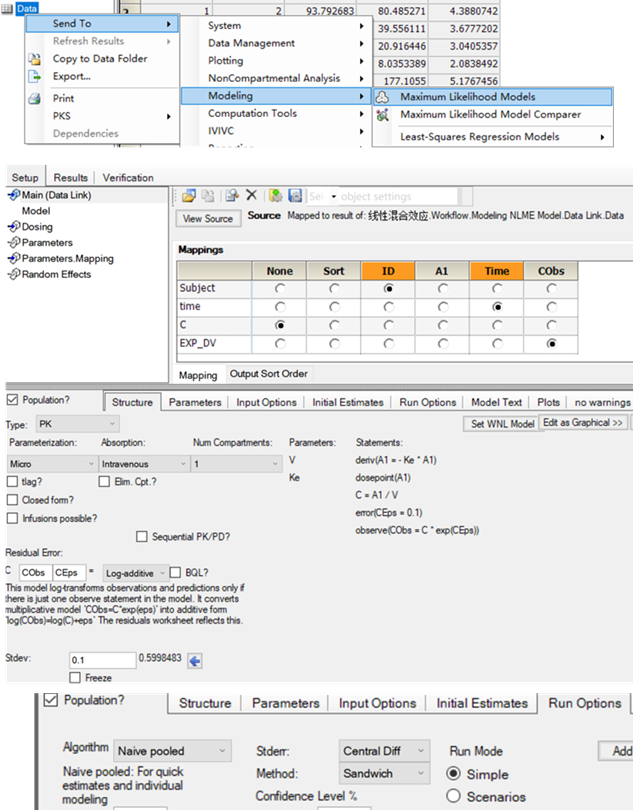
3.1.2NLME模型构建
所使用的PK模型
𝑑A/𝑑𝑡=-𝑘𝑒∗A
𝐶=𝐴/𝑉
log(C_obs)=log(C)+ε
Phoenix中的操作
-
将数据集发送至“最大似然模型(Maximum Likelihood Models)”操作对象
-
将EXP_DV映射值“浓度观测值(CObs)”字段
-
将time映射至“时间(time)”
-
在“结构(Strucure)”选项卡,将PK模型指定为“微观(Micro)”参数化,“血管内(Intravenous)”,1房室模型。
-
误差模型设定为“对数加和型(Log-addtive)”
-
将subject映射至“ID”字段
-
将算法设定为“单纯积聚法(Naïve pooled)”
3.1.3结果:
LME结果:
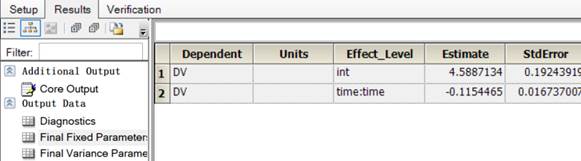
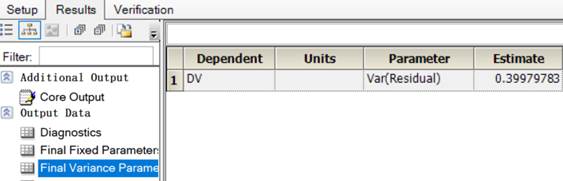
整理后:
| 参数 | 值 |
|---|---|
| Ke | 0.1154465 |
| V | 10.165929 |
| Var(Residual) | 0.3997978 |
NLME的结果:
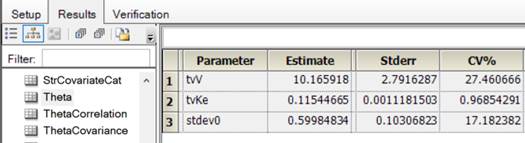
整理后得:
| 参数 | 值 |
|---|---|
| tvV | 10.165918 |
| tvKe | 0.11544665 |
| stdev0 | 0.59984834 |
| Var(Residual) | 0.35981803 |
3.2将个体层面的变异作为固定效应引入模型
3.2.1.LME模型构建
统计学模型:
Ln(Conc)=int +time* β1+subject* β2+ε
Phoenix中的操作
-
将数据集发送至线性混合效应模型操作对象
-
将DV映射值“因变量(Dependent)”字段
-
将time映射至“回归字段(Regressor)”
-
将subject映射至“分类变量(Classification)”字段下
-
在“固定效应(Fixed Effect)”选项卡,将time,subject指定为固定效应
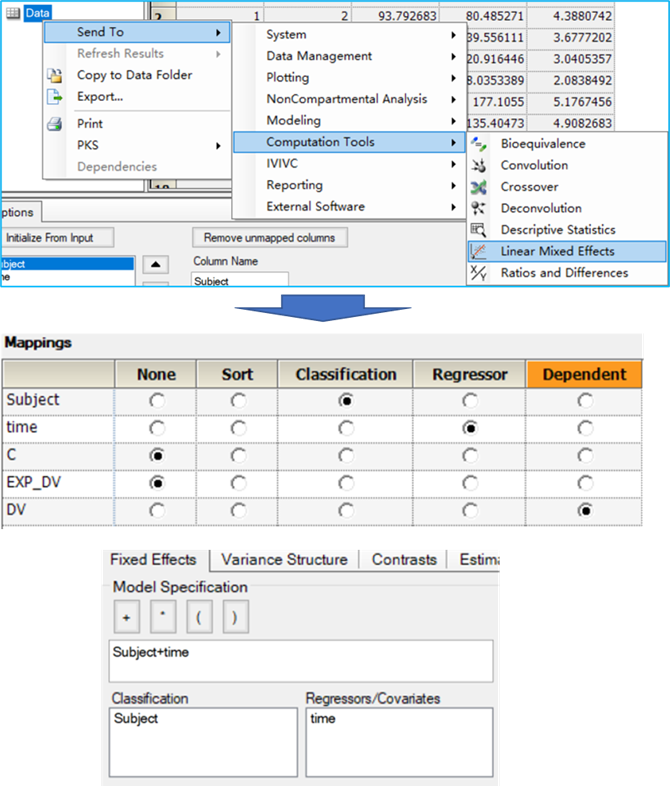
3.2.2NLME模型构建
以将个体作为固定效应引入模型中并不是Pop PK常用方法,也与两步法有差异,所以不在“ML Model”操作对象中实现了,但作为用于直观理解两步法,LME的模型足够了。
3.2.3结果
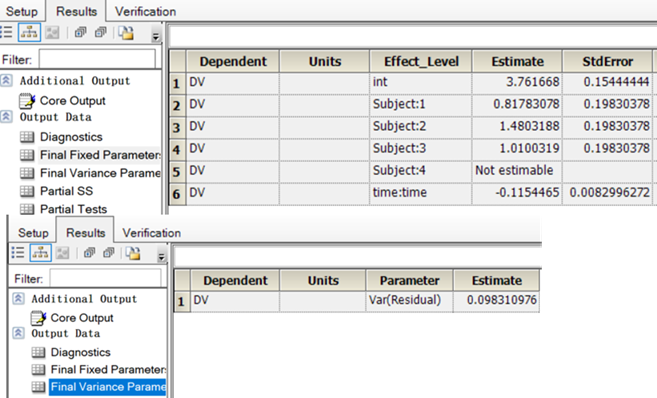
整理后:
| 参数 | 值 |
|---|---|
| V4 | 23.244934 |
| V3 | 8.4659761 |
| V2 | 5.2897363 |
| V1 | 10.260037 |
| Ke | 0.1154465 |
| Mean_V | 11.81517085 |
| Var(Residual) | 0.098310976 |
3.3将个体层面的变异作为随机应引入模型
3.3.1LME模型构建
统计学模型:
Ln(C)=int+timeβ+subjectγ+ε
Phoenix中的操作
-
将数据集发送至线性混合效应模型操作对象
-
将DV映射值“因变量(Dependent)”字段
-
将time映射至“回归字段(Regressor)”
-
将subject映射至“分类变量(Classification)”字段下
-
在“固定效应(Fixed Effect)”选项卡,将time指定为固定效应
-
在“方差结构(Variance Structure)”选项卡下,将Subject指定为随机效应
3.3.2 NLME模型构建
dA/dt=-Ke*A
C=A/V
log(C_obs)=log(C)+ε
V=tvV+nV
nv~N(0,ω^2)
Phoenix中的操作
-
将数据集发送至“最大似然模型(Maximum Likelihood Models)”操作对象
-
将EXP_DV映射值“浓度观测值(CObs)”字段
-
将time映射至“时间(time)”
-
将subject映射至“ID”字段下
-
在“结构(Strucure)”选项卡,将PK模型指定为“微观(Micro)”参数化,“血管内(Intravenous)”,1房室模型。
-
误差模型设定为“对数加和型(Log-addtive)”
-
在“参数(Parameter)”→“结构(Structural)”选项卡下,取消ke的随机效应复选狂。
-
将算法设定为“FOCE”
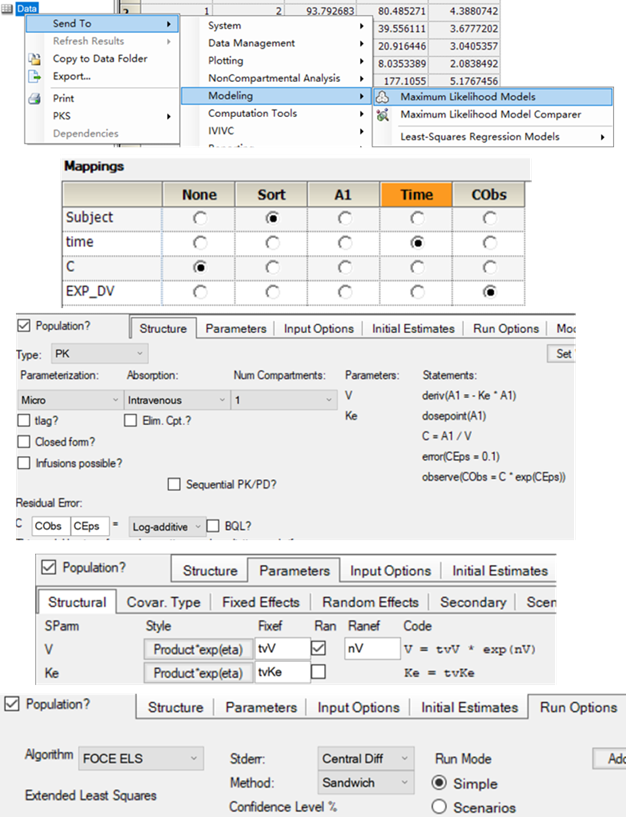
3.3.3结果
LME的结果
整理后:
| 参数 | 值 |
|---|---|
| Ke | 0.115446497 |
| V | 10.16592915 |
| Var(Subject) | 0.36178422 |
| Var(Residual) | 0.098310976 |
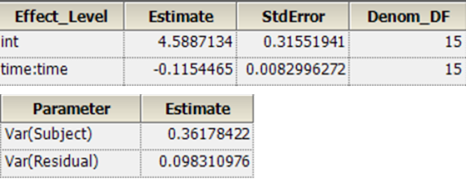
NLME的结果:
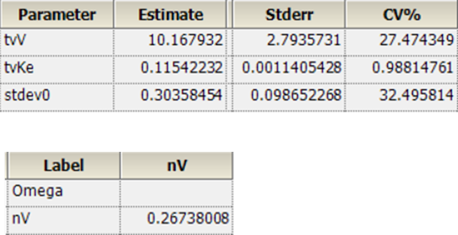
整理后:
| 参数 | 值 |
|---|---|
| tvV | 10.167932 |
| tvKe | 0.11542232 |
| stdev0 | 0.30358454 |
| Var(Residual) | 0.092163573 |
| VAR(nV) | 0.26738008 |
4.一些备注说明
关于“Linear Mixed Effects”操作对象与“ML Model”操作对象间的一些差异说明:
Phoenix的“Linear Mixed Effects”操作对象,使用限制性最大似然法构建目标函数;“ML Model”操作对象使用最大似然法构建目标函数。
限制性最大似然与最大似然法之间存在着一些差异,一个明显的区别是结果中的估算出的方差值,一般限制性最大似然的比最大似然的大,这是由于自由度的差异导致的。
两步法的说明:
两步法在这里和Pop PK传统的两部法不同,因为按照传统的视角,是确确实实将每个个体分开拟合的,而将个体作为固定效应引入模型后,比如本模型,其确实会为每个个体估计了一个单独的V,但是所有个体共享一个Ke和残差,所以这与传统的不同,在ML Model中也能实现类似的方式描述模型,但这非本次重点,感性取得小伙伴可以自己尝试构建下。
5.随堂作业
大家可以尝试一下练习:
使用LME构建一下模型:
-
将斜率的个体间差异作为固定效应引入模型。
-
将斜率的个体间差异作为随机效应引入模型。
-
同时将截距与斜率的个体间差异作为随机效应引入模型。
使用“ML Model”构建一下模型:
- 2*2生物等效性的统计学模型
